5 おまけ
5.1 よくある質問
Q1. ごたくはいいから、使い方だけ教えろや。
A1. そういう態度はあまり感心しませんが、まあいいでしょう。 第3.1項を読んでください。
■
Q2. わたしが解析しようとしているデータでは、 反応時間の分布が負に歪んで(左に尾を引いて)います。 ex-Gaussian分布の歪曲の成分はパラメータによって決まるとのことですが、 fitexGauss関数における推定時には、 の値は0以上を想定しているようです。 が負の値をとっても良いようにすることで、 負に歪んだデータにもex-Gaussian分布のフィッティングを適用することはできないでしょうか。
A2. できません。
ex-Gaussian分布におけるパラメータは、 もとの指数分布のパラメータです。 そしてこの値は、定義上0より大きな値しかとることができません。 (が負の場合、指数分布の定義は確率密度分布としての制約を満たしません。) よってex-Gaussian分布では、正に歪んだ分布しかフィッティングすることができません。
もしどうしてもex-Gaussian分布と相同の分布で負に歪んだデータをフィッティングしたければ、 正規分布と指数分布にしたがう独立な確率変数の(和ではなく) 差がしたがう分布を考えるとよいかもしれません。 この分布は、ex-Gaussian分布をちょうど左右に反転したようなかたちになります。
par(mfrow=c(2, 1)) x <- rnorm(10000) y <- rexp(10000) hist(x + y, breaks=100) hist(x - y, breaks=100)
ただし、適切なタイムプレッシャーをかけた課題において、 反応時間が負に歪むことは通常考えられません。 解析をひねる前に、 あなたの実験がそもそも反応時間を解析するのに適切な構成になっていたか、 よく考えてみたほうがよいでしょう。
■
Q3. 最尤推定が収束しないので結局つかいものになりません。 推定を安定させる方法はありませんか?
A3. 最尤推定以外のフィッティング方法を試すとよいかもしれません。
本文中でも強調したとおり、 最尤推定は 「実際に観察された現象を生み出しそうなパラメータを推定値とする」 という簡潔な思想に基づく推定方法です。 その理屈は単純ながら説得力があり、 また数学的にも優れた性質をもつことが知られています。 そのため本解説文では、 単にRのoptimの使い方を説明するだけというのではなく、 最尤推定の原理や思想を学習できるよう、 少し詳しくとりあげました。
しかし一方で、 最尤推定法は必ずしも万能というわけではありません。 とくに問題となるのはハズレ値による影響です。 最尤推定法は実データにおける観察を重視する手法であるため、 必然的にハズレ値に弱く、 少数のハズレ値によっても推定されるパラメータが大きく乱れることが知られています。 なかでも反応時間分布解析においては、 短潜時の早い反応によるハズレ値の影響が深刻です。 というのもex-Gaussian分布は、 遅い反応時間が一定量含まれ、 右に尾をひくかたちで正に歪んだデータを想定した分布です。 そのためサンプル内に遅い反応時間が含まれるぶんには、 予定どおりそれをパラメータとして吸収できます。 しかし非常に早い反応時間については、 正規分布成分の分散にあたるを広げて対応するほかなく、 それによって肝心な分布の尾の部分は実データと齟齬が大きくなり、 Figure 14でみたように推定精度が悪くなってしまうのです。
こうした最尤推定の弱点に対応するため、 fitexGauss関数には、 最尤推定以外に2種類の別の推定方法を追加しました。 ひとつは理論分布から計算した分位点により実データを階級化し、 計算される統計量を最小化する、 すなわち分割表における差が最小になるようなパラメータを探す方法。 もうひとつは、 同じく実データと理論分布の差の指標であるコルモゴロフ-スミルノフ統計量(KS統計量) を用い、 これを最小化するようなパラメータを探すという方法です。 これらの方法について本文のように詳しく取りあげることはしませんが、 察しのよい方はこの説明だけで、 第3.9項および第3.10項でとりあげた議論 (データと理論分布の一致性)との類似にピンとくるでしょう。 すなわちこれらの推定法では、 本文中において「データが理論分布にどれだけあてはまっているか」 を測るために使った指標を利用し、 それを最大にするex-Gaussian分布のパラメータを算出することで、 理論分布を実データにもっともマッチするようにフィッティングを行ないます。 プログラム上では、 最尤推定において尤度関数を指定したfnを、 代わりに統計量またはKS統計量として定義しただけです。
最尤推定はサンプル内のすべての観測値を平等にあつかうため、 少数含まれるハズレ値に大きな影響を受けました。 それに対し、統計量は階級化の過程で、 KS統計量は累積密度分布のy軸方向のズレを指標とすることで、 もとの反応時間データに含まれていた極端なハズレ値の影響を受けにくくなります。 一方、 起こりうるハズレ値に強くなるということは、 つねにデータのなかから一定量の情報を捨てていることに他ならないため、 ハズレ値のないサンプルにおいては、 これらの方法のほうが最尤推定よりも精度が悪くなる可能性もあります。
試しにex-Gaussian分布に従う様々なサンプルサイズの擬似データを生成し、 上記の3方法でどのような推定結果が得られるかを試してみました(Figure 16)。
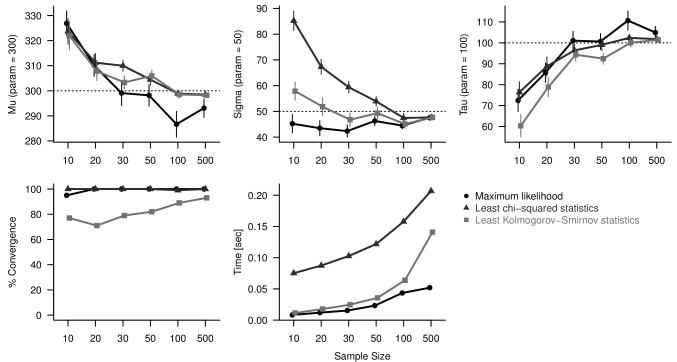
5つのパネルはそれぞれ、 推定された・・の値と、 推定計算の収束率、推定に要した時間を示す。 横軸は1回のフィッティングに使用する反応時間のサンプルサイズ。 点線はrexGauss生成時に指定した真のパラメータの値を示す。 黒色: 最尤推定法 濃灰色: 統計量最小化法 淡灰色: KS統計量最小化法
横軸がサンプルサイズを表わし、 5つのパネルが順に、推定されたパラメータ、 パラメータ、パラメータ、 推定計算の収束率、推定にかかった時間の平均値を示しています。 いずれの方法を用いた場合も、 サンプルサイズが500と極端に大きければ、 すべてのパラメータをほぼ正確に推定できています (点線が擬似データ生成時に指定した真のパラメータの値)。 統計量を用いた方法(濃灰色)では、 分位点を用いる特性上ハズレ値に強く、 小さなサンプルサイズでも収束率は100%に近いですが、 その代わりに計算時間が長くなっています。 KS統計量を用いた方法(淡灰色)では、 計算時間は比較的抑えられていますが、 小標本だと推定計算が収束しないケースが多いようです。 これらに対し、 最尤推定の結果得られた推定値は他の方法と大差なく、 かつ安定した収束率と計算時間を達成しています。 このことから、 データがex-Gaussian分布にしたがっている限りは、 とりあえずデフォルトの最尤推定法を用いても大きな問題はなさそうです。
では前出の議論のように、 極端に早い反応時間が含まれるデータではどうでしょうか。 Figure 17は、 本文中のFigure 14で提示したものと同じデータに、 改めて3つの方法で推定計算を行なった結果を示したものです。
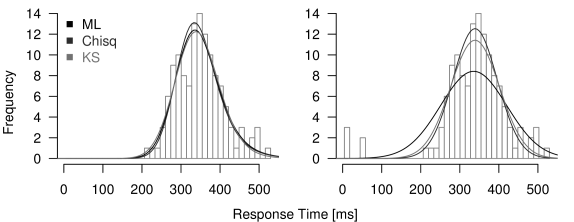
最尤推定では、 少数含まれるハズレ値に推定結果が大きな影響を受けやすい。
左図のように、 標準的なex-Gaussian分布をとるデータ(ヒストグラム)に対しては、 どの推定方法もおなじような理論分布(曲線)をはじきだします。 このおなじデータに、 極めて早い反応時間のデータを5試行分だけ追加し、 もう一度推定をした結果が右図です。 先にFigure 14でみたとおり、 最尤推定法はこの手のハズレ値に弱く、 この例ではがほぼ0と推定されてしまったのでした(黒色)。 それに対し他の方法では、 早いハズレ値の影響がないとはいえませんが、 明らかに最尤推定よりも程度が抑えられていることがわかります。 このように、最尤推定法だとハズレ値の影響が深刻になるケースでは、 いま紹介した他の推定法を試してみる価値があるでしょう。 fitexGauss関数において、 こうした推定方法の切り替えはtype引数で行なうことができ、 "ml"・"chisq"・"ks"のいずれかを指定することで、 尤度・統計量・KS統計量を用いた推定方法を選択します。
■
Q4. 歪曲した分布をもつデータを扱うための方法なんだから、 平均3SDを超える点を除外するなどの前処理はまったく必要ないんですよね?
A4. そう言いきれないのが実際のデータの悩ましいところです。
反応時間分布の解析は、反応時間データにおける 「だいたいある値ぐらいになるけれど、 そこそこ遅いケースもぼちぼち見受けられる」という特徴をもとに、 それをex-Gaussian分布のパラメータにより定量するという方法でした。 よって、「どうも遅い反応が多かったから3SD1515 どうでもいいけど、3SDってとっさに3DSにみえますよね。 以上のデータを全部切ってから解析した」 といった安直な前処理は、当然推奨されません。
しかしだからといって、 そういったハズレ値の前処理が絶対に不要かというと、 そうも言いきれません。 とくにうえの質問にもあったとおり、 ex-Gaussian分布を使った最尤推定は短い潜時のハズレ値に非常に敏感です。 Figure 14の例においては、 推定計算後のフィッティング精度のについて調べることで、 そういった推定のうまくいかないデータセットは除外できる、 と説明しました。 しかし実験協力者や課題構成によっては、 極端に早い反応の試行が紛れ込みやすい状況もあり得ます。 そういったハズレ値が(割合としては非常に少なかったとしても) どの協力者でも1–2回ぐらいは出てしまっているような状況では、 本文にしたがってデータセットを捨てていくと、 使えるデータがほとんどなくなってしまうでしょう。 そのため、フィッティングがうまくいかないデータを頭ごなしに捨てるのではなく、 そうした悪影響を与えそうなハズレ値は取り除いてから分布解析をするという工夫も、 現実場面では必要になってきます。
これはなにも早い反応時間のハズレ値に限ったことではありません。 たしかにex-Gaussian分布を用いた解析は、 反応時間分布の尾の部分に注目するという意味で、 低頻度で起こる遅い反応も「大事にする」解析方法といえます。 でも単純反応課題で5秒とか10秒とかいう反応時間の試行があったら、 さすがにハズレ値とみなすべきだと思うでしょう。 それは刺激を見逃したとか、 瞬間的に寝ていたとかいう別の要因によってもたらされたものであり、 課題遂行に要する認知過程を反映して生じる反応時間分布の歪みとは、 質的に異なるものだと考えられるからです。 もちろんそうしたハズレ値は、 推定される分布の歪曲(パラメータ)を不当に大きく見積もらせる原因となるので、 可能であればデータの前処理によって取り除いておきたい代物です。
すると今度は当然、 どの程度の極端な値ならハズレ値として除外すべきかが問題になります。 しかしこれに明確な解答はありません。 筆者自身は、平均値から4–5SDもハズレた反応時間というのは、 なにか別の原因がない限り考えにくいと思っています。 ある知人は3SDを超えたら除外するのがよいといっていました。 これらいずれもあくまで主観的・経験的な判断であって、 なぜその値で区切るのかという絶対的な根拠はありません。 また当然ながら、 どんな課題であるかによっても事情は異なります。 課題の性質として、 一部の試行で本当に(課題遂行にともなう正当なプロセスとして) 反応時間が極端に早かったり遅かったりする場合もあり得ます。 結局のところ、 「何SDより外側をハズレ値とすればよいか」 に汎用の答はないのです。
この問題に関して、個人的には、 生じてしまったハズレ値をあとから取り除くのではなく、 そもそもそういったデータが混ざり込まないよう課題を工夫しておくほうが、 実用上価値が高いと考えています。 たとえば刺激の呈示に対して協力者に反応で報告させる課題の場合、 試行内での各イベントのタイミングが一定の間隔に固定されていると、 課題を繰り返すなかで協力者に反応のタイミングを学習されてしまいます。 そうなると、 刺激が呈示されるよりまえから反応をはじめるといった「フライング」が起こり、 数十ミリ秒といった信じられない反応時間がとれてしまいます。 これは課題内イベントの起こるタイミングを試行ごとにランダムに変動させ、 協力者が反応のタイミングを予測できなくすることで防ぐことができます。 また、そもそも物理的な制約として、 人間がなんらかの判断をして実際の骨格筋の運動を遂行し終えるまでに数十ミリ秒なんてことは、 人体の構造上なかなか考えられることではありません。 よって、たとえば50ミリ秒以下の反応時間が得られた場合、 それは協力者が「正しく」課題を遂行していなかったしるしとみなし、 その試行を最初から誤答としてしまうのも有効です。 さらに課題における難易度をあげたり、 求められる反応の種類を増やすことで、 あてずっぽうで反応した場合に正答となる偶然水準を下げると、 協力者により慎重な反応戦略を課すことができます。 このようにして協力者の課題遂行戦略をより保守的になるよう工夫すると、 極端に早い反応時間のハズレ値はある程度抑止することができます。
遅すぎる反応時間についても、 早すぎるものと同様、 課題のつくりとして最初から誤答にしてしまうのが有効です。 たとえば刺激呈示から800ミリ秒以内に反応しなければならない課題なら、 データ上800ミリ秒以上の反応時間が得られることはあり得ません。 こうした時間制限をかけておくことは、 極端に大きなハズレ値を抑制するだけでなく、 適切なタイムプレッシャーをかけることで、 課題条件ごとの分布特徴の差を観察しやすくする効果もあります (第1.2項参照)。 ただしあまりにも厳しい時間制限を課してしまうと、 それによって協力者の課題への取り組みかたが大幅に変わり、 おなじ課題を使った先行研究と結果が全然違うといったことにもなりかねません。 解析方法と違い、 実験実施の方法はあとから変えるということができません。 よって正反応とみなす反応時間に関する制限は、 実験計画の段階で慎重に吟味しておく必要があるでしょう。
お気づきのとおり、 これらの方法は結局のところ、 ハズレ値の除去を実験実施の時点で先にやっておいているだけです。 そのため最終的には、 あとからハズレ値を除去する場合の 「なにをハズレ値とみなすべきかの基準がない」 という悩みとおなじ問題にぶつかってしまいます。 よってどちらのやりかたをするかは、 もはや好みの問題というべきかもしれません。 個人的には、 解析をする時点になってから思いもよらぬハズレ値に閉口して3SDを切り捨てるくらいなら、 最初から課題条件に工夫をしておくほうが好みです。 かといって、 いくらハズレ値が出にくいように課題を工夫しておいたとしても、 結局はハズレ値まみれのデータが得られてしまい、 解析前にデータの前処理をしなければならなくなることもあり得ます1616 とくに動物実験の被験体は、 得てして実験者の思惑にまったくそぐわない行動をするものです。。 前半で結論したのとおなじく、 やはりこの問題に汎用の解はないのです。
現実的な落としどころとしては、 ハズレ値のせいでフィッティングうまくいかないケースに遭遇してしまったら、 まずはさまざまな基準値でのハズレ値の除外とフィッティングを試し、 最低限のデータの除外で充分なフィッティング精度が得られるハズレ値のカットオフを探しましょう。 単に「慣習にのっとって3SDより外側はすべて捨てた」 という思考停止なやり方をするのではなく、 ハズレ値の基準を段階的に変化させると、 それによってどのような値の観測値(早い?遅い?) がどの程度(何試行?全体の何%?)除外され、 フィッティング精度がどのように向上したのかを、 最低限、自分では把握しておくべきです。 Q-Qプロットの決定係数やKS検定の結果といった数字を読むだけでなく、 実データのヒストグラムと推定された理論分布の一致具合を目で確認することもとても重要です。 さらに可能であれば、 ハズレ値の除外によって解析がどのような影響を受けるのかや、 何にもとづいて最終的なカットオフ値を採用したのかについても、 論文中か補足資料中に記載できるとなおよいでしょう。 論文中に「実験者が目でみて確認しました(visually inspected)」 と書くのは、いかにも主観的な表現で不安なものです。 しかしハズレ値の基準を変えた場合のフィッティングへの影響の定性(願わくば定量)や、 それによってどのようなデータが除外されたのかという確かな数字の報告とともに併記される 「最終的にはよいフィッティングが得られていることを実験者の visual inspectionによっても併せて確認しました」 という文言は、 少なくともマイナスにはたらくことはないと個人的には思います。 優れた研究者ほど、 いかにももっともらしい統計値を盲目的に信頼することの危険と、 生のデータを目で観察することの重要性をよく知っているものです。
■
Q5. 各協力者の条件ごとの試行数が少なすぎて、 フィッティングがうまくいきません。 なにかよい解決策はないでしょうか。
A5. 慣習的に行なわれている、いくつかの方法があります。
ex-Gaussian分布解析を行なおうとしたとき、もっともネックになるのは、 このサンプルサイズの問題ではないでしょうか。 本文中で説明したとおり、ex-Gaussian分布によるパラメータの最尤推定には、 計算機による繰り返し演算が必要になります。 すなわち、ほんの少しずつパラメータを変化させ、 それによる尤度の変化を調べることで、 尤度がより大きくなるほうへとパラメータをじりじり動かしていきます。 そして、 パラメータをその周辺でどのように変化させても尤度がいまより下がってしまうような点を、 尤度関数の極大値とみなし、 それを与えたパラメータの値を推定値として採用するのです。 このとき多くの最尤推定アルゴリズムでは、 パラメータの微小変化に対して尤度の変化量が十分少ないこと、 すなわちその点で尤度がある程度収束していることを、 計算終了の目安としています。
しかしながらフィッティングに用いたデータのサンプルサイズが小さい場合、 尤度関数がそもそも滑らかでなく、 いつまでたっても尤度が収束せずに推定が終わらないことがあります。 これはex-Gaussian分布解析に限らず、 最尤推定を利用した解析方法にはつねに起こりうる問題です。 そのため、解析において最尤推定を使う場合には、 それに足るだけのデータを集めなければならないのです。
ex-Gaussian分布はいちおう、 比較的少ないサンプルでもそれなりのフィッティングができるということになっています。 しかしそれでも、1回の推定でせめて100程度のサンプルサイズがないと、 コンスタントにきれいなフィッティングを得ることはできません。 そのため多くの心理学実験、とくに知覚心理学や心理物理学と比べ、 条件ごとの試行数がそれほど多くない認知心理学のような分野では、 事前にex-Gaussian分布解析を見越して実験計画を立てていたのでもない限り、 信頼性の高いフィッティング精度をすることは難しくなります。 これがこの解析方法を試してみようとおもったとき、 現実的にぶち当たるもっとも大きな障壁となります。 どんなにヘタに実験計画を組み、 条件あたりの試行数が少なかったとしても、 各課題条件での平均反応時間が求められないということはありません。 もちろんサンプルサイズが小さければ、 それだけ統計学的な信頼性は劣ることになりますが、 それでも平均値はいちおう計算可能です。 それに対してex-Gaussian分布解析では、サンプルサイズが小さいと、 そもそもパラメータの推定値を算出することができないのです。 そのため、この解析を使おうと思っても、 試行数の制約のために使えないということもあるのではないでしょうか。
そのような場合、いちおう慣習的に利用されてきたいくつかの解決策があります。 ひとつは、無作為に数人ずつの実験協力者の生データをグループにまとめ、 それをひとりのsupersubjectのデータとしてフィッティングする方法です。 たとえば実際の実験データにおいて、 各協力者、条件ごとに50試行ずつしかないのであれば、 より正確なフィッティングに必要な100というサンプルサイズをかせぐために、 2人ずつの協力者をまとめてしまいます。 協力者1・2はsupersubject A、協力者3・4はsupersubject Bといった具合です。 こうしてつくられたsupersubjectそれぞれを、 あたかも単一の協力者であったかのように、 普通にフィッティングにかけます。 このとき、1人のsupersubjectを構成したもとの2人の協力者のデータは、 もはや区別されません。 この方法はかなり乱暴にみえますが、 実験協力者間で条件による反応時間の傾向が一致しているのであれば、 それなりによくデータを定量することができます。 ただしその推定結果が、特定のグループ化の結果に依存しないことを示すため、 何度も別の組み合わせでsupersubjectをつくりなおし、 質的に同じ推定が得られることを確かめる必要があります。
サンプルサイズが小さい実験デザインにおいて分布解析を行なうもうひとつの方法は、 VincentizeまたはVincent averaging と呼ばれる手法を用いることです。 Vincentizeは、 各実験協力者について適当な細かさの分位点を計算し、 それを協力者間で平均することで、 協力者全体での反応時間のヒストグラム(グループヒストグラム)を得る方法です。 分位点の数はデータに依存しますが、 一般に生データの解像度よりも細かな分位点は意味がないので、 もとの条件ごとのサンプルサイズよりも小さな値になります。 先の各条件50試行ずつのデータの例でいえば、たとえば協力者ごとに、 二十分位点(5%刻みの分位点)を計算します。 そしてそれぞれの分位点を協力者間で平均し、 グループ全体での分位点とします。 これを横軸にプロットし、縦方向には、 この分位点のあいだを埋めるように同一面積の長方形を描けば、 全体のヒストグラムを得ることができます。 このヒストグラムをex-Gaussian分布でフィッティングすることにより、 パラメータの推定値を計算するのです。 Code. 5.5に、 Vincentizeによるグループヒストグラム作成のための簡単なプログラム例を載せておきますので、 参考にしてください。 先ほどのsupersubject化の方法と合わせ、 まず協力者を適当なsupersubjectにまとめ、 それぞれでVincentizeによってパラメータを推定したあと、 推定値をsupersubject間で平均する、 という方法もあります。
このように、ex-Gaussian分布解析におけるサンプルサイズの問題には、 いちおうの解決策があります。 ただ、筆者の個人的な意見としては、 これらの方法はあくまで次善の策であって、 手放しでオススメできるものではありません。 やはり反応時間に関して信頼できるフィッティング精度を得たければ、 実験計画の段階で、 それに見合うだけの試行数が集められるような工夫が必要と思います。
■
Q6. 条件Aと条件Bでのフィッティングの結果を比べたら、 条件Bにおいての値が有意に大きくなっていました。 これをもとに、条件Bのほうがより課題の難易度が高かったと結論できますか。
A6. 論じることは可能ですが、それをもって証拠とすることはできません。
ex-Gaussian分布を用いたフィッティングによる解析は、 平均値や標準偏差を算出するだけの解析よりも、 一見すると複雑で高次なことをしているようにみえます。 またたしかに、データがなんらかの理論モデルに基づいた分布によってフィッティングされるなら、 特定のパラメータの条件間での変化を、 そのモデルにおけるパラメータの機能と直接結びつけて議論することができるでしょう。 そのような解析の実例としては、 ランダム・ドット・モーション課題を用いた近年の認知神経科学研究があげられます。 この実験系においては、課題において必要とされる心理過程が、 拡散モデルやLATERモデルといった数理アルゴリズムとして確立されています。 よってそのようなモデルでデータをフィッティングした場合、 パラメータにみられた条件間での差を、 モデルにおけるパラメータの機能から直接に解釈することが可能です。 たとえばある課題条件においてパラメータの推定値が増加していたとき、 もともとの数理モデルにおいては「内的な証拠に対する基準値」 であるとすれば、 協力者がこの条件ではより保守的な戦略をとったという解釈が可能になります。
しかし第2.2項や第2.3項で述べたとおり、 反応時間のフィッティングに利用される分布はいずれも、 データがその分布にしたがうという明確な根拠はもちません。 これらの理論分布は、正に歪曲し、 反応時間データと類似した分布型をもつという経験的な理由から利用されているだけです。 すなわち、本解説文で紹介したフィッティングを用いた解析も、 一般的な平均や標準偏差をもちいた数値要約と同様、 単なる記述的な意味しかもたないのです。 よって、理論分布でフィッティングしたからということを理由に、 特定のパラメータを特定の心理機能に直接結びつけて議論することはできません。
もちろん、「ある条件でex-Gaussian分布のの推定値が大きくなっており、 これは課題条件間の難易度の差を反映したものと考えられる」というような考察は、 可能だとは思います。 実験で得られた結果をまとめ、 そこから実際に起きていた心理過程について考察するというのは、 すべての実験心理学研究において必要とされる、 正当な研究の手続きだからです。 しかし、パラメータの推定値はあくまで平均や標準偏差と同様の 「結果の記述」であり、 心理過程を考察するうえで、 何らかの「根拠」として無条件で意味をもつようなものではないことを、 心に留めておいてください。
■
Q7. 一般にデータ解析においては、 代表値(e.g. 平均値)とばらつきの指標(e.g. 標準偏差)という2つの指標を使います。 しかしex-Gaussian分布を用いたフィッティングでは計3つのパラメータを指標としています。 説明のためのパラメータを増やせば、 データをよりよく説明できるのは当たり前のことではないですか? 単にデータをよくフィッティングできればよいのなら、 パラメータを100個とか使ってフィッティングすればよいということになりませんか?
A7. 少し思い違いをされているようですね。そういうハナシにはなりません。
理論分布のフィッティングによってデータを定量するとき、 オーバーフィッティング overfitting (過剰適合)の可能性はつねに問題となります。 たとえば多項式による回帰分析を行なう場合、 一般的に次数をあげればあげるほど、 数値上のフィッティングのよさは向上します。 同じx座標をとらないn個の点は、n-1次式を使えば全点を通ることができるため、 「完璧な」フィッティングが可能です。 しかしそのようなことをして非常に高次の多項式でデータを回帰しても、 その回帰係数の値の解釈はほとんどできないでしょう。 たとえば「データを37次式で回帰した結果、 という関係が見出された」といわれても、 そこから何がいえるのかさっぱり分かりません。 このように、説明のためのパラメータ数をむやみに増やすと、 数値上のあてはまりのよさは向上するものの、 データのもつ性質を理解するのには役に立たなくなってしまいます。 このような問題をオーバーフィッティングと呼びます。
たしかに、ex-Gaussian分布は3つのパラメータによって分布形状が決まるため、 平均と標準偏差という2指標での定量よりも精度があがるのは、 当然といえるかもしれません。 しかし注意してほしいのは、ex-Gaussian分布による解析は、 先の多項式の例と異なり、 無尽蔵にパラメータを増やしてデータをオーバーフィッティングしたりはしないということです。 というのもex-Gaussian分布は・・ という3つのパラメータによってEq.2.3のように定義されている分布です。 これ以上パラメータを増やしても減らしても、 それはもはやex-Gaussian分布とはいえません。 よってex-Gaussian分布を用いた解析が、 4個以上のパラメータを使用してデータをオーバーフィッティングすることはあり得ません。
では、平均・標準偏差の2指標から、・・の3指標になったことは、 オーバーフィッティングではないのでしょうか。 それは、実際のデータを扱ってみればすぐに分かります。 本文中で聞き飽きるほどいってきましたが、 一般に反応時間のデータはたいてい正の歪曲をもちます。 そしてそのようなデータにおいては、平均値にしろ中央値にしろ最頻値にしろ、 単一の代表値だけでは、 明らかに分布のもつピークと尾というふたつの情報は伝えきれません。 またばらつきに関しても、 標準偏差は左右対称な分布をとるデータでしか意味をもちません。
このように、平均と標準偏差という2指標は、 反応時間のデータを要約するには明らかに不十分なのです。 その理由は、ひとえに分布の歪曲というデータの特徴です。 そこで、分布の「位置」と「ばらつき」という2つの観点に加え、 分布の歪曲にあたる「尾の引き具合」という3つめの観点として導入されるのが、 パラメータだといえます。 すなわち、ex-Gaussian分布の第3のパラメータは、 既存の数値要約では扱いきれなかったデータの特徴に対応するため、 狙いすまして打たれた一手だといえるでしょう。 2指標でそもそも定量しきれていなかったものが、 3指標にすることで見事に評価できるようになったわけですから、 これはオーバーフィッティングとはいいません。
まとめると、ex-Gaussian分布を用いた分布解析は、 2指標による定量よりも明らかに多くの情報を抽出でき、 またこれ以上のパラメータをむやみに導入することもありません。 反応時間解析に利用される分布の多くが3パラメータをもっていることからも、 このパラメータ数が反応時間データの定量のための必要かつ十分な数であることが分かると思います。
■
Q8. フィッティングを用いた解析は、 途中に「理論分布へのあてはまり具合」という段階を踏むため、 やはり単純な平均値や標準偏差をつかった解析と比べて恣意的な (「小細工をしている」という)印象を与えませんか? だとすれば、手法として問題は含んでいたとしても、 せいぜい変数変換をして、 通常の分散分析を用いた解析にとどめておいたほうが良くはないでしょうか。
A8. そのような印象を与えうることは否定はしません。 しかし実は、あなたが「普通の」と思っている平均値や標準偏差といった指標にも、 世間一般に信じられているほどの根拠はないということに注意してください。
たしかに、ex-Gaussian分布を用いたフィッティングは、平均値や標準偏差の算出と比べると、 必要とされる計算の手順が多く複雑です。 また先述のとおり、この手法自体はそれほど新しいものでもないのですが、 研究者のプログラミング能力の不足やデータの歪曲に対する問題意識の欠如のため、 それほど一般に浸透しているわけではありません。 そのため、たとえば学会発表や論文などで唐突に ex-Gaussian分布を利用した反応時間解析をもちだすと、 聴衆や読者に不必要に怪しまれてしまうことも充分考えられます。 「平均値では結果が出ないから、ややこしい解析もちだしてきやがったな」 「平均値のような基本的な指標でちゃんと出てないってことは、 信頼できる結果ではなさそうだ」と。 よってそのような反応を受けるくらいなら、 反応時間分布の歪曲の問題は認識しながらも、 戦略的に平均と標準偏差のみを用いて話をするという態度もあり得ると思います。
しかしそれでは、平均値や標準偏差、 あるいはノンパラメトリクスなら中央値や四分位範囲といった指標は、 理論分布のフィッティングによる推定値よりも 「基本的」で「信頼できる」指標なのでしょうか。 たとえば平均値は、すべての観測値を足し合わせ、 それをサンプルサイズで割った値です。 しかし、通常の平均では単純に全サンプルを足し合わせますが、 それぞれのサンプルに別々の係数をかけたのちに足し合わせる、 重み付き平均というものも存在します。
こう考えると、われわれがいつも使っている平均値というものは、 すべての観測値の重みを1にした、 重み付き平均の非常に特殊な場合ということができます。
中央値についてはどうでしょうか。 中央値とは、データ全体を二分する (上側50%と下側50%に分ける)境となる値のことです。 しかしデータを切り分ける方法は、当然ながら二等分だけではありません。 データを四分割する境の点は四分位点と呼ばれ、 第1四分位点はデータを下側25%と上側75%に分ける点、 第3四分位点は逆に下側75%と上側25%に分ける点です。 百等分する点を考えれば百分位点となります。 百分位点という視点からみれば、 中央値は第50百分位点(下から数えて50番目の百分位点)と呼ぶことができるでしょう。 ではなぜ、第50百分位点はデータ要約において重要な代表値として特別扱いされ、 第49百分位点や第51百分位点は使えないのでしょうか。
もちろん多くのひとは、これらのいちゃもんに対して、 「重み付け平均や第49・51百分位点よりも、普通の平均値や中央値のほうが、 データを平等に利用していて恣意的でない」という反論をするでしょう。 しかし、その「平等」とか「恣意的」という理由は、 あくまで人間の意味的判断によるものであって、 「俺は納得できる」という主張以上のものではないのです。 不偏性や頑健性などの数理的特徴を用いて議論することもできるでしょうが、 すべての統計ユーザが、 不偏性という数理的性質のために平均値を選択し、 中心極限定理のためにパラメトリクスを選択しているとは到底思えません。 多くのひとは、単に「自分が自然に納得できる」というだけの理由をもって、 平均値や中央値、 標準偏差や四分位範囲などの指標を選択しているように思えます。 もしそうだとすれば、データの要約にどんな指標を用いるのがよいかは、 その人物の理解力や数学的センスに制約されることになります。
結局わたしがいいたいのは、 皆さんが信じてやまない平均値などの「一般的」な指標も、 じつはそれほど確固たる理由をもって使われているわけではない、ということです。 これらの指標が万人に受け入れられている理由は、 万人がこの指標の定義になんとなく納得できるから、 ぐらいのものなのではないでしょうか。 意地悪な言いかたをすれば、 堪え性も数学的教養もない一般聴衆の「最大公約数」を想定したとき、 そのセンスでついてこられる計算のレベルが平均値であり、 標準偏差であるのでしょう。 そして筆者は、これがひとつの真理ではないかと思っています。 データ解析は、数値要約にしろフィッティングにしろ、 生データに何らかの処理を加えて人間に解釈しやすくするという意味ではどれも同じです。 そして解析の結果は、 「処理の結果どれだけ解釈しやすくなったか」と 「処理は妥当なものだったか」というふたつの天秤によってはかられます。 さらに究極的には、このふたつの論点は、 いずれも「結果をみる側にとって、それをどれだけ認められるか」 という問題に集約されます。 解析に使った手法は認めてもらえても、 それによりでてきた結果が学術的にまったく面白くなければ、 意味はありません。 逆にどんなに興味深い結果を示そうとも、 解析に使った手法があまりにも複雑で理解に苦しむものでは、 やはり誰も振り向いてくれないでしょう。 解析結果そのもののもつ意味と、 それを抽出するために使った方法の理解しやすさというふたつのバランスのなかで、 聞き手に理解され受け入れられる折衷点を探さなければならないのです。 戦略的にex-Gaussian分布解析を用いないということも考えられる、と最初に述べたのは、 このような思想が筆者のあたまのなかにあったからでした。
実験によって得られたデータは、 いつだって「そのデータ」たったひとつです。 しかしそれに対して可能な解析は無数に存在し、 「必ずこうすればよい」というような万能解は存在しません。 筆者個人としては、まとめの項でも書いたとおり、 そこに存在する差を見逃さないということがもっとも重要だと考えており、 そのためにex-Gaussian分布解析は有用なツールだと思います。 しかしときと場合によっては、あえてそれを用いないほうがよいことだってあるでしょう。 導き出される情報とその抽出のための手法の分かりやすさというふたつの観点のあいだで、 あなたのデータのもつ意味をもっとも効率的に伝えられる解析方法を選び出してください。
5.2 付録1: exGauss.R
rexGauss <- function(n, mu=300, sigma=50, tau=50) {
return(rnorm(n, mu, sigma) + rexp(n, 1/tau))
}
dexGauss <- function(x, mu=300, sigma=50, tau=50, log=FALSE, limit=10^-4) {
if (tau < limit) {
d <- dnorm(x, mean=mu, sd=sigma, log=TRUE)
} else {
d <- log(1 / tau) - (x - mu) / tau + (sigma^2) / (2 * (tau^2)) +
pnorm((x - mu) / sigma - sigma / tau, 0, 1, log.p=TRUE)
}
if (!log) {
d <- exp(d)
}
return(d)
}
fitexGauss <- function(
rt, # A vector of RTs to analyze distribution
type = c("ml", "chisq", "ks"), # Fitting procedure
probs = seq(0.1, 0.9, by=0.2), # Quantiles for chisq procedure
warn = FALSE, # Whether to print warnings in optim
maxit = 1000, # Maximal number of iteration in optim
qmax = 100, # Maximal number of quantiles in Q-Q plot
... # Additional arguments for optim
) {
type <- type[1]
rt <- rt[!is.na(rt)]
nrt <- length(rt)
arg <- list(...)
arg$control$maxit <- maxit
# 1st - 3rd cumulants
k <- rep(NA, 3)
k[1] <- mean(rt)
k[2] <- var(rt)
k[3] <- mean((rt - k[1])^3)
# Estimates of ex-Gaussian parameters by moment statistics
momfit <- c(mu=NA, sigma=NA, tau=NA)
momfit[3] <- ifelse(k[3] > 0, (k[3]/2)^(1/3), 10^(-5))
momfit[1] <- k[1] - momfit[3]
v <- k[2] - momfit[3]^2
momfit[2] <- ifelse(v > 0, sqrt(v), 10^(-5))
# Definition of function to minimize in optim
if (type == "ml") {
# Sign-inverted sum of prob density (in log scale)
fn <- function(THETA) {
THETA <- exp(THETA)
return(-sum(dexGauss(rt, THETA[1], THETA[2], THETA[3], TRUE)))
}
} else if (type == "chisq") {
# Chi-squared statistics in contingency table
n_lev <- 1:(length(probs) + 1)
n_pred <- diff(c(0, probs, 1)) * nrt
fn <- function(THETA) {
THETA <- exp(THETA)
q <- c(-Inf, qexGauss(probs, THETA[1], THETA[2], THETA[3]), Inf)
n_obs <- table(cut(rt, breaks=q, labels=n_lev))
return(sum(((n_obs - n_pred) ^ 2) / n_pred))
}
} else if (type == "ks") {
# Y-axis discrepancy in cumulative prob dist
rt_sorted <- sort(rt)
p <- seq(1 / nrt, by=1 / nrt, length.out=nrt)
fn <- function(THETA) {
THETA <- exp(THETA)
return(max(abs(pexGauss(rt_sorted, THETA[1], THETA[2], THETA[3]) - p)))
}
}
optold <- options(warn=ifelse(warn, 0, -1))
init <- momfit
init <- log(init)
loglikefit <- optim(par=init, fn=fn, arg)
param <- loglikefit$par
param <- exp(param)
options(optold)
if (FALSE) { # To check the failure in moment estimates
if (any(momfit == 10^(-5))) {
cat("fitexGauss: Moment estimate for sigma or tau became 0\n")
print(matrix(c(momfit, param), byrow=TRUE, nrow=2,
dimnames=list(c("mom","loglike"), c("mu","sigma","tau"))))
}
}
rtnvalue <- list(mom=momfit, loglike=param,
optimrslt=loglikefit[-1], convergence=loglikefit$convergence, rt=rt)
class(rtnvalue) <- "htest.exGauss"
# Calculate r^2 in Q-Q plot
if (nrt > (qmax+1)) {
# qmax-tiles should be separated by qmax+1 points
# Require qmax+3 seps to eliminate lower and upper limits
# which are -Inf and Inf in the theoretical CDF
obs <- quantile(rt, probs=seq(0, 1, length.out=qmax+3))
} else {
obs <- sort(rt)
}
l <- length(obs)
pred <- qexGauss(seq(0, 1, length.out=l),
param["mu"], param["sigma"], param["tau"])
obs <- obs[-c(1, l)]
pred <- pred[-c(1, l)]
rtnvalue$lmrslt <- lm(obs~pred)
s <- summary(rtnvalue$lmrslt)
rtnvalue$r.squared <- s$r.squared
# Kolmogorov-Smirnov Test
rtnvalue$ksrslt <- suppressWarnings(ks.test(rt, pexGauss,
mu=param["mu"], sigma=param["sigma"], tau=param["tau"]))
return(rtnvalue)
}
pexGauss <- function(q, mu=300, sigma=50, tau=50,
lower.tail=TRUE, log.p=FALSE) {
mayinf <- -(q-mu)/tau
if (any(is.infinite(exp(mayinf)))) {
# Practically equal to Gaussian distribution
# when tau is very small
p <- pnorm((q-mu)/sigma)
} else {
p <- pnorm((q-mu)/sigma) - exp(mayinf +
(sigma^2)/(2*(tau^2)) + log(pnorm((q-mu)/sigma - sigma/tau)))
}
if (!lower.tail) {
p <- 1 - p
}
if (log.p) {
p <- log(p)
}
return(p)
}
qexGauss <- function(p, mu=300, sigma=50, tau=50,
lower.tail=TRUE, log.p=FALSE) {
if (log.p) {
p <- exp(p)
}
if (!lower.tail) {
p <- 1 - p
}
if (any(c(p < 0, p > 1))) {
stop("qexGauss: <p> must be from 0 to 1")
}
pfunc <- function(x) {
pexGauss(x, mu=mu, sigma=sigma, tau=tau)
}
m <- mu + tau
bin <- ifelse(p > pfunc(m), 1, -1) * mean(c(sigma, tau))
q <- mapply(FUN=function(p_tmp, b_tmp) {
if (p_tmp == 0) {
return(-Inf)
} else if (p_tmp == 1) {
return(Inf)
}
cri <- m
while (sign(pfunc(cri) - p_tmp) == sign(pfunc(cri + b_tmp) - p_tmp)) {
cri <- cri + b_tmp
}
func <- function(r){ pfunc(r) - p_tmp }
return(uniroot(func, sort(c(cri, cri + b_tmp)))$root)
}, p, bin)
return(q)
}
plot.htest.exGauss <- function(
x,
y = NA,
main = "",
xlab = "Time [ms]",
ylab = ifelse(freq, "Frequency", "Density"),
border = "black",
ylim = NULL,
freq = TRUE,
breaks = 30,
plot = TRUE,
...
) {
rt <- x$rt
fit <- x$loglike
# Draw histogram
histrslt <- hist(rt, breaks=breaks, plot=plot,
border=border,
main=main, xlab=xlab, ylab=ylab,
ylim=ylim, freq=freq)
if (x$optimrslt$convergence == 0) {
# Density function with fitted exGauss parameters
# xlim <- range(histrslt$breaks)
xlim <- par("usr")[1:2]
x <- seq(xlim[1], xlim[2], length.out=100)
y <- dexGauss(x, fit["mu"], fit["sigma"], fit["tau"])
if (!freq) { # Density plot
h <- 1
} else { # Frequency plot
h <- max(histrslt$counts) / max(histrslt$density)
}
lines(x, y * h, ...)
}
invisible()
}
5.3 付録2: exampleRT.R
nsub <- 15
source("exGauss.R")
set.seed(100)
word <- c(rep(rep(c("red", "green"), 2), each=50), rep(c("xxx", "xxxxx"), each=50))
color <- rep(c("red", "green", "green", "red", "red", "green"), each=50)
cond <- rep(c("cng", "incng", "neut"), each=100)
proto <- data.frame(word=word, color=color, cond=cond)
err <- function(
eprob # Probability of error
) {
sample(c(0,1), 100, replace=TRUE, prob=c(eprob,100-eprob))
}
dir.create("./data", showWarnings=FALSE)
options(warn=-1)
makesample <- function(sub) {
mu <- c(500, 600, 520) + rnorm(3, sd=10) + rnorm(1, sd=50)
sigma <- c(50, 110, 50) + rnorm(3, sd=5) + rnorm(1, sd=10)
tau <- c(110, 115, 90) + rnorm(3, sd=5) + rnorm(1, sd=10)
RT <- round(as.vector(mapply(FUN=rexGauss, 100, mu, sigma, tau)))
cor <- as.vector(sapply(FUN=err, X=c(3,15,5)))
tmp <- proto
tmp$RT <- RT
tmp$cor <- cor
tmp <- tmp[sample(1:300),]
tmp$trial <- 1:300
tmp <- tmp[,c("trial", "word", "color", "cond", "RT", "cor")]
filename <- paste("./data/sub_", sub, ".txt", sep="")
con <- file(filename, open="w")
textout <- c("Pseudo-data of Stroop task for ex-Gaussian RT analysis",
"Experimenter\tSatou Tanaka",
paste("Experimental date\t", Sys.Date()-nsub+sub, sep=""))
writeLines(text=textout, con=con, sep="\n")
cat("\n", file=con)
close(con)
write.table(tmp, file=filename, append=TRUE, sep="\t", quote=FALSE,
col.names=TRUE, row.names=FALSE)
}
lapply(X=1:nsub, FUN=makesample)
options(warn=0)
5.4 付録3: analyzeRT.R
nsub <- 15 # Number of subjects
source("exGauss.R")
histRT <- function(
rt, # List[3] containing RTs for each condition
leg, # List[3] containing 5 stats & params for each condition
nbin=30 # Number of bins in the histograms
) {
ylim <- c(min(unlist(rt)), max(unlist(rt))+1)
br <- seq(ylim[1], ylim[2], length.out=nbin)
leg <- round(leg)
prefix <- c("Mean:", "SD:", "Mu:", "Sigma:", "Tau:")
hist(rt$cng, breaks=br, main="Congruent")
legend("topright", legend=paste(prefix, leg[1,]), bty="n")
hist(rt$neut, breaks=br, main="Neutral")
legend("topright", legend=paste(prefix, leg[2,]), bty="n")
hist(rt$incng, breaks=br, main="Incongruent")
legend("topright", legend=paste(prefix, leg[3,]), bty="n")
}
analyzeSub <- function(filename) {
sub <- matrix(NA, nrow=3, ncol=5) # Container for statistics and estimates
tmp <- read.table(filename, header=TRUE, skip=4)
cor <- tmp[as.logical(tmp$cor),] # Correct trials only
cond <- cor$cond
RT <- cor$RT
RT <- split(RT, cond)
sub[,1] <- sapply(X=RT, FUN=mean)[c("cng","neut","incng")]
sub[,2] <- sapply(X=RT, FUN=sd)[c("cng","neut","incng")]
sub[1,3:5] <- fitexGauss(RT$cng)$loglike
sub[2,3:5] <- fitexGauss(RT$neut)$loglike
sub[3,3:5] <- fitexGauss(RT$incng)$loglike
histRT(RT, sub)
return(sub)
}
statRT <- function(
param, # Matrix[ncond, nsub] containing estimates of one parameter
title # Name of the parameter
) {
param <- data.frame(RT=as.vector(param), cond=rep(c("cng","neut","incng"), nsub),
sub=rep(paste("sub", 1:nsub, sep=""), each=3))
rsltaov <- aov(RT ~ cond + sub, data=param)
title <- paste("### ", title, " ###", sep="")
cat(paste(c(rep("#", nchar(title)), "\n"), collapse=""))
cat(title, "\n", sep="")
cat(paste(c(rep("#", nchar(title)), "\n\n"), collapse=""))
cat("### ANOVA ###\n\n")
print(summary(rsltaov))
cat("\n")
cat("### TukeyHSD ###\n\n")
print(TukeyHSD(rsltaov, "cond"))
}
postscript("histRT.eps", width=3, height=6, paper="special", horizontal=FALSE)
par(mfrow=c(3,1), mar=c(3,4,3,1), las=1)
rslt <- lapply(FUN=analyzeSub, X=paste("./data/sub_", 1:nsub, ".txt", sep=""))
dev.off()
rslt <- array(unlist(rslt), dim=c(3,5,nsub))
mstats <- apply(X=rslt, MARGIN=c(1,2), FUN=mean)
sstats <- apply(X=rslt, MARGIN=c(1,2), FUN=sd)
postscript("paramRT.eps", width=5, height=5, paper="special", horizontal=FALSE)
x <- barplot(mstats, beside=TRUE, names.arg=c("mean","SD","mu","sigma","tau"),
legend.text=c("congruent","neutral","incongruent"), las=1)
x <- as.vector(x)
mmax <- as.vector(mstats + sstats)
mmin <- as.vector(mstats - sstats)
# arrows(x, mmax, x, mmin, code=3, angle=90, length=0.05) # For error bars
dev.off()
sink("statrslt.txt")
mapply(FUN=statRT, list(rslt[,1,], rslt[,2,], rslt[,3,], rslt[,4,], rslt[,5,]),
c("Mean", "SD", "Mu", "Sigma", "Tau"))
sink()
5.5 付録4: vincentize.R
vincentize <- function(
rt, # List[N] containing RTs for N subjects
n=20, # Number of quantile
xlim=NA,
...
) {
vin <- function(x) {
return(quantile(x, prob=seq(0, 1, length.out=n+1)))
}
quan <- lapply(X=rt, FUN=vin)
quan <- do.call(rbind, quan)
mquan <- colMeans(quan)
uarea <- 1 / n # Unit area
h <- uarea / diff(mquan)
if (is.na(xlim[1])) {
xlim <- range(mquan[-length(mquan)])
}
plot(0, 0, type="n", xlim=xlim, ylim=c(0, max(h)),
xlab="", ylab="Probability Density", ...)
rect(mquan[-length(mquan)], 0, mquan[-1], h)
invisible(list(quan=quan, mquan=mquan))
}





 @kanri_ninjin
@kanri_ninjin



 イクナイ! 581
イクナイ! 581