3 Rによるex-Gaussian分布解析の実装
前節までで、反応時間解析における一般的な問題と、 フィッティングを使った分布解析の概要を説明した。 本節では、これを読んでいるあなたが 「じゃあ実際に反応時間データを解析してみよう」と思ったときどのようにすればよいかを、 Rにおけるプログラムの実例と実習をとおして学習する77 Matlabとかいう腐れ言語を使ってるひとのことは知りません。 また本解説文に付録したRコードをMatlabへと移植する等の迷惑行為の一切はこれを禁じます。 また必要に応じて、プログラミングだけでなく、 統計学的な手法についての補足解説も行なっていく。 これにより、ex-Gaussian分布でのフィッティングを用いた反応時間解析を、 単なる机上の知識ではなく、 自分で使える道具として習得するのが、本解説文の最終的な目標である。
3.1 とりあえず使ってみよう
いま現在、実際に解析したい反応時間データをもっている読者は、 何はともあれ早くフィッティングによる解析の方法が知りたいかもしれない。 ということで、ものは試しともいうし、 とりあえずex-Gaussian分布を用いた反応時間データのフィッティングをやってみよう。 この時点では何をやっているかよく分からないかもしれないが、 詳しくは追って説明していくので心配しなくてよい。
反応時間解析に用いる一連の関数のコードは、 http://noucobi.com/Rsource/exGauss.R に単一ファイルとしてまとめてある。 この関数群は筆者がつくった自作関数なので、 普通にRを起動しただけでは使うことはできない。 そこでまず、リンクからexGauss.Rを保存するか、 本解説文末尾の付録Code. 5.2の内容をコピー&ペーストして、 読み込むファイルを用意する。 その後Rを起動し、現在のディレクトリ内に上記のファイルを置いたうえで、
source("exGauss.R")
を実行して、関数をR上にロードする。 これにより「ほにゃららexGauss」と名の付く一連の関数群が読み込まれた。 一般にRにおける確率分布関数群は、 d・p・q・rのそれぞれではじまる4種の関数がセットになっている。 たとえば正規分布を意味するnorm系の関数は、 dnorm・pnorm・qnorm・rnormの4つでひと揃いである。 これらの関数群は、 その理論分布の確率密度(d)・ 累積密度(p)・ 確率点(q) およびその分布にしたがう乱数(r)を取得する機能を提供する。 ex-Gaussian分布に関してもこの慣習にのっとり、 dexGauss・pexGauss・ qexGauss・rexGaussという4つの関数を準備した。 さらにこれらの関数を利用して、 指定されたデータにex-Gaussian分布のフィッティングを行なう関数がfitexGaussである。 ぶっちゃけていえば、fitexGaussに解析したいデータを放り込めば、 ex-Gaussian分布でフィッティングして、推定されたパラメータを返してくれる。
では、実際にやってみよう。 自分で解析したいデータがあるひとは、 適当な変数(xとしよう)にベクトルとしてデータを入れておく。 とくになければ、以下の手順により、 rexGaussを使って擬似データをつくる。
(x <- rexGauss(200)) summary(x) hist(x, breaks=20)
これによりxに200試行分の反応時間の擬似データが格納された。 これを、
fitexGauss(x)[1:2]
のように単純にfitexGaussに与えてやれば、 フィッティングの結果がコンソールに表示される。 (fitexGaussは3番目以降の返り値として、 フィッティングの収束などに関する詳細な情報を返してくるが、 いまはそれらの情報があると見づらいので、 [1:2]によって推定された結果のパラメータだけを表示している。) 擬似データをつくるのに使用したrexGaussは、 とくに指定しなければ、、 となるようにデータを生成するから、 フィッティングの結果これに近い値が返ってきていれば、 データの特徴をex-Gaussian分布のパラメータとして正確に定量できたことになる。 出力において、$mom以下のものと$loglike以下のものは、 それぞれ別の方法を用いてパラメータを推定した結果を示しており、 詳細は以下の項で詳しく説明していく。 たまたま発生された擬似データに依存してフィッティングの結果は違うだろうが、 rexGaussによる乱数生成と fitexGaussによるフィッティングを何度か繰り返せば、 だいたいは実際のパラメータに近い値が推定できていることが分かるだろう。
3.2 ex-Gaussian分布にしたがう乱数の発生
さて、ではここから、 ex-Gaussian分布を用いてデータをフィッティングするための方法を説明していこう。 具体的には、 さきほどexGauss.Rファイルから読み込まれた関数群のうち3つについて、 それらを作成する過程とその意味を、順を追って説明していく。 まず本項では、 ex-Gaussian分布の定義をおさらいするため、 ex-Gaussian分布にしたがう乱数を発生する関数rexGaussの中身をみてみよう。
Rにおいて乱数発生関数は、 rnormやrunifのように「rほにゃらら」と命名され、 発生したい乱数の数nと、 その乱数がしたがう分布のパラメータを与えて呼び出す。 ここでつくるのはex-Gaussian分布にしたがう乱数を発生する関数ので、 rexGaussと名付けることにしよう。 このような関数は、単にデータをフィッティングするだけならば必要ない。 しかし乱数発生関数は、前項で行なったようなテストデータの生成にも使えるし、 なによりこれを作成する過程でex-Gaussian分布の生い立ちをよりよく理解することができる。
とはいえ、じつはex-Gaussian分布にしたがう乱数の発生はすこぶる簡単である。 ex-Gaussian分布の定義を思い出してほしい。 ex-Gaussian分布は、正規分布にしたがう確率変数と、 指数分布にしたがう確率変数の和がしたがう分布であった(Eq.2.3)。 Rでは、正規分布にしたがう乱数はrnorm、 指数分布にしたがう乱数はrexpで得ることができる。 よって、これらの和は、ex-Gaussian分布にしたがうことになる。
X11(width=9, height=3) par(mfrow=c(1, 3)) x <- rnorm(10000) y <- rexp(10000) hist(x, breaks=50) # Normal hist(y, breaks=50) # Exp hist(x + y, breaks=50) # exGauss
あとは、必要な乱数の数nと、 任意のパラメータ値・・ を与えられるように関数として整理すれば、 Code. 5.2内のrexGaussの定義のようになる。 各パラメータの省略時既定は、 とりあえず一般的な反応時間データとして観察されるくらいの適当な値に設定しておいた。
注意として、Rでは指数分布のパラメータを、 分布の平均値ではなく、 の逆数として与えなければならない。 しかしex-Gaussian分布を使ううえでは、 やはり指数分布部分の平均としてののかたちでパラメータを扱ったほうが直感的である。 そこでrexGaussでは、引数においてはを与え、 内部でその逆数をrexpに渡すようにしている。
では、せっかくできたので、 何度か異なるパラメータでex-Gaussian分布にしたがう乱数を発生してみよう。
X11(width=4.5, height=9)
par(mfrow=c(3, 1))
n <- 1000
f <- function(x) {
x <- x[(x > 0) & (x < 1500)]
hist(x, breaks=seq(0, 1500, by=50))
}
f(rexGauss(n, 500, 100, 50))
f(rexGauss(n, 500, 200, 50))
f(rexGauss(n, 500, 100, 200))
を大きくすると、 分布の位置や歪曲はそのままで、 ピークまわりの裾野のひろがりだけが大きくなる。 まただけを大きくすると、 分布の尾だけが右に伸びるように変化している。
また、 ex-Gaussian分布のパラメータと、 それにしたがう確率変数の統計量との関係についても確認してみよう。 ex-Gaussian分布においては、 ・・という3種のパラメータと、 データから計算される平均・分散・歪度という3つの指標の関係が Eq.2.3のように決まっているのだった。 そこで、 ・・のex-Gaussian分布を考えると、 予想される平均・分散・歪度は
mu <- 300
sigma <- 50
tau <- 100
cat("mean = ", mu + tau, "\n",
"var = ", sigma^2 + tau^2, "\n",
"skew = ",
2 * tau^3 / ((sigma^2 + tau^2) ^ (3/2)),
"\n", sep="")
となる。 一方、おなじパラメータ値から乱数を生成してみる。 歪度の計算式はEq.1であることに注意すると、 データから実際に計算される平均・分散・歪度は
x <- rexGauss(10000, mu, sigma, tau)
m <- mean(x)
v <- var(x)
cat("mean = ", m, "\n",
"var = ", v, "\n",
"skew = ", mean((x - m)^3) / (v^(3/2)),
"\n", sep="")
となる。 歪度の実値はズレが大きくなることも多いが、 何度か乱数発生を繰り返してみれば、 おおよそはパラメータからの予想と一致することがみてとれる。
3.3 ex-Gaussian分布の確率密度関数
前項ではex-Gaussian分布にしたがう乱数発生のための関数を作成した。 本項ではex-Gaussian分布の確率密度関数をR上に定義していこう。 Rにおいて確率密度関数は、 dnormやdpoisのように「dほにゃらら」と命名され、 x軸上の値xを与えると、 分布からその値が取り出される確率の密度(離散分布の場合は確率そのもの)を返す (Figure 9)。
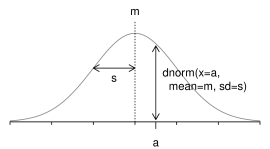
dnorm関数は、 平均m標準偏差sの正規分布において、 x=aの点での確率密度関数の高さを返す。
もちろん、分布のパラメータは関数呼び出し時に指定してやる必要がある。 ここではex-Gaussian分布の確率密度関数をdexGaussとして定義する。 これは最尤法によってフィッティングを行なうために不可欠な関数となる。
ex-Gaussian分布の確率密度関数の数学的定義は、 すでにEq.2.3で示した。 残念なことに、これはTable 1で例示した5つの分布の確率密度関数のなかでも、 一番ややこしそうだ。 しかし安心してほしい。 実際のところ、これをR上に定義するのはみためよりよほど簡単である。
Eq.2.3の確率密度関数が難しそうにみえるのは、 その定義のなかに積分が含まれているためだろう。 逆にいえば、この積分の部分さえ処理してしまえば、 ・・はただの定数だから、 何のことはない普通の数値演算である。 そこで、まずはEq.2.3を少し変形して、
| (6) | ||||
とする。 これは単に、前に出ていた定数項を積分のなかにいれただけだ。 しかしこうすると、少し見通しがきいてくる。 よくみればわかるように、この式の後半部分は、 標準正規分布の下側確率になっているからだ。 標準正規分布とは、平均0分散1の正規分布のことであるから、 その確率密度関数はEq.2に、を代入して
| (7) |
である。 まさにいま求めたいEq.6 の積分部分の中身と同じかたちになっている。 これをからまで積分したもの、 すなわち標準正規分布におけるより左の部分の面積が、 Eq.6の後半部分になる。 Rにおいて正規分布の下側確率(あるよりも左側の部分の面積) はpnormによって得られるから、 結局これは
| (8) |
で求めることができる。 ・・・などは関数呼び出し時にユーザから指定された既知の値、 ようするに定数だから、Eq.8はRでそのまま計算可能である。
ここまでくれば、dexGaussの定義は終わったも同然だ。 ようはxと必要なパラメータmu・sigma・tauを引数として受け取り、 単純にEq.6の式を計算して返せばよいだけだ。 積分の部分は、上述のとおりpnormを用いて計算すればよい。 Code. 5.2の2段落目にあるdexGaussが、 これを実際に定義した例となる。 この定義では、上記の4つに加えlogという引数を用意しており、 これによって確率密度ではなく、 確率密度の自然対数を返すこともできるようにした。 これは後述の最尤法を用いたパラメータ推定での利便性のためだ。
ではさきほどの乱数発生関数と同様、 ここではいまつくった確率密度関数を使って、 異なるパラメータでex-Gaussian分布を描いてみよう。
X11() i <- seq(0, 1500, 10) plot(0, 0, type="n", xlim=c(0, 1500), ylim=c(0, 0.004)) lines(i, dexGauss(i, 500, 100, 50)) lines(i, dexGauss(i, 500, 50, 200)) lines(i, dexGauss(i, 750, 200, 1))
3つめの例からわかるように、 の値が非常に小さい場合、 ex-Gaussian分布の確率密度分布は正規分布のそれとほとんど変わらなくなる。 指数分布成分の平均値が非常に小さいと、 分布の尾が引かなくなるのだから当然である。 この場合でも、 確率密度の算出においては、 単純にその小さな値のをEq.6 にそのまま放り込んでやればよいだけだ。 式の定義上、 が小さくなるにつれて Eq.6は自然にEq.2に近づいていく。
3.4 ex-Gaussian分布の累積密度関数と確率点
exGauss.Rファイルのなかには、 ここまででみてきた乱数発生関数(rexGauss) と確率密度関数(dexGauss)のほかに、 累積密度関数(pexGauss) と確率点関数(qexGauss)の定義も記載されている。 これらの関数は、後述のフィッティング精度の計算などに必要となるので、 確率密度関数などと同時に定義しておいてある。 しかし累積密度や確率点の算出は、 本解説文の中心となるパラメータの最尤推定の過程においては不要なため、 これらの関数の内部実装を前2者の関数のように詳細に説明することはしない。 実際、pexGaussやqexGaussが本項以降に本文中に出てくることはない。
いちおう簡単に説明しておくと、 pexGaussはex-Gaussian分布の下側積分値をもとめる累積密度関数である。 ex-Gaussian分布の累積密度関数は、 を標準正規分布の累積密度関数とすると、
で定義される。 それをそのままプログラムにしたのがpexGaussである。 ただしこの式は指数計算時に無限大に飛びやすいので、 その部分に関して若干の条件分岐判別を行なっている。 qexGaussは確率()を指定することで、 累積密度がその値となるような確率変数値(確率点)をもとめる関数である。 しかしex-Gaussian分布において累積密度関数の逆関数は導出できないので、 qexGaussはpexGaussを繰り返し実行し、 その返り値が指定された確率と等しくなる点を探す。 そのためqexGaussは、 数式に基づいて数値計算を行なうだけの他の3種の関数と比べると低速である。
3.5 モーメント統計量によるパラメータ推定
では、いよいよex-Gaussian分布によるデータのフィッティングのための関数、 fitexGaussの作成に取りかかろう。 第3.1項で体験してもらったように、この関数は、 試行ごとの反応時間データをベクトルとして与えると、 それをex-Gaussian分布でフィッティングして推定されたパラメータを返す。 しかしフィッティングといってもその方法はさまざまある。 本解説文では、 まず本項でモーメント統計量とパラメータの関係を利用した推定法を解説し、 さらに次項でそれをもとにして最尤推定を行なう方法を述べる。
モーメント統計量 moment statisticsとは、 われわれがデータの定量のため慣習的によく用いる、 平均・分散・歪度・尖度などの指標の総称である。 数学が苦手なひとにはちょっと読み飛ばしてもらうことにしつつ、 数学がお嫌いでない読者諸氏のために書いておくと、 この「モーメント」という名称は、 確率変数Xに関して、その平均をm、標準偏差をsとすると、 これらの指標が一般に、r次のモーメント
や、原点まわりのr次のモーメント
あるいはr次の標準化モーメント
のかたちをもつためである。 (モーメントの記号は、 正規分布のパラメータのとはまったく関係ない。 単に統計学における慣習として、 モーメント・原点まわりのモーメント・標準化モーメントを、 それぞれ・・の記号で表記することになっているだけだ。) とはいえ、 ここではべつにそのような統計学的知識を要求しているわけではないから、 安心してほしい。 ようするに、 データから計算できるこれらの指標とex-Gaussian分布のパラメータとの関係を利用して、 フィッティングをしてやろうということだ。 ここまでの実習をちゃんと行なってきた理想的な読者のみなさんなら、 第3.2項での乱数発生関数を定義したあとに、 ex-Gaussian分布における統計量(平均・分散・歪度) とパラメータの関係を確認したことを覚えているだろう。 あれと同じことを、 統計量は実データから計算できるが、 パラメータは未知であるという状態で行なうというのがここでの目標だ。
おさらいの意味も込めて再掲すると、ex-Gaussian分布では、 分布のパラメータと平均・分散・歪度との関係が
のように決まっているのだった。 これはこの分布がもつ数学的な性質である。 一方、これらの指標は当然ながらデータから直接計算することができ、 サンプルサイズnのデータxにおいて、
| (9) | ||||
である。 よってこれらの3式をそれぞれ連立させれば、
| (10) | ||||
という3つの方程式が得られる。 これらの式を、データベクトルxに対するRのコードを含めて表現すれば、
| (11) | ||||
ということになる。 未知の変数が3個で式が3本あるので、あとはこれを連立方程式として解けばよい。 すなわち、まずは一番下の式から
でが求められ、さらに
でとが求められる。 これを実際にR上で定義したものが、 Code. 5.2におけるfitexGaussの前半部分である。 ex-Gaussian分布の定義からかつなので、 計算上これらのパラメータの推定値が正とならない場合には、 かわりに非常に小さな正の値(10-5)とした。
このように、 ex-Gaussian分布におけるパラメータとモーメント統計量の数学的関係を利用することで、 実データから計算された統計量を使って、 分布のパラメータを推定することができる。 しかし、このようにして得られたパラメータの推定値は、 一般にハズレ値に大きく影響されることが知られており、 実際のデータ解析のうえでは、それがしばしば問題となる。 たとえば、データに少数の極端に大きな値が含まれるとき、 は非常に大きな値となり、 その結果、が過大に見積もられる。 するとやは、との関係上、そのぶん小さく推定されてしまう。 とくには、の推定値が大きいと、 ほとんど0になってしまうことも少なくない。 しかし実際の反応時間データにおいて、 正規分布部分の裾野の広がりがないということはあり得ず、 この推定が正しくデータを定量できていないことは明らかである。
以上のように、モーメント統計量を用いたパラメータの推定は非常に簡単であるが、 ハズレ値に弱いという欠点をもつ。 そこで次項では、 より洗練された方法を用いてex-Gaussian分布によるデータのフィッティングを行なう方法を説明する。
3.6 最尤推定法
本項では、前項で紹介したモーメント統計量でのパラメータ推定に代わる方法として、 最尤法を用いたフィッティングを学習する。 ただし本解説文は統計学の初学者を読者として想定しているため、 本論にはいるのに先立って、 まずは最尤法一般に関する簡単な説明を行なう。 そのあとで、実際にRを用いて最尤推定を行なうための方法を解説する。 「最尤法なんて聞かなくとも知っとるわ」という向きは、 次項まで飛ばしていただいて構わない。
最尤推定法 maximum likelihood estimation (最尤法)は、 尤度を指標として、データともっとも一致する理論分布のパラメータを探し出す方法である。 数学の教科書にありがちなお堅い言いまわしで申し訳ないが、 すぐ下でていねいに説明するので、 数学嫌いのかたもいましばらく辛抱していただきたい。 尤度 likelihoodの「尤」は訓読みすると「もっとも」と読む88 学部生時代、 友人とふざけて「犬度(いぬど)」と呼んでいた。 狼男がどのくらい狼化しているかを表わす指標に違いない。。 よって尤度とは、くだいていえば「もっともらしさ」の指標である。 その尤度を最大化する手続きこそが、最尤推定法である。 だから字面どおりに読みくだせば、 最尤法によって推定されるパラメータは 「もっとも(最も)もっとも(尤も)らしい」推定値ということになろう。
ではその尤度とは、数学上、いったいどんなものなのか。 「数学的にもっともだ」とはどういう状況のことを指すのか。 例を用いながら説明しよう。 たとえばあなたが、なんらかの実験によってサンプルサイズのデータを得たとする。 なんでも構わないのだが、 たとえばペットとして飼っているカエルの回の跳躍距離のデータとしよう。
というようなデータである。 データの分布はおよそ平均30標準偏差5で、 平均値を中心に正規分布状のなだらかな分布になっていたとする。
最尤法では、 まずデータを生みだしたもとの分布(母分布)やそのパラメータを仮に決め、 そこから実際に観測されたデータが得られる確率を計算する。 この例では、 データが正規分布様だという観察があった想定なので、 仮定する母分布は正規分布でよいだろう。 またパラメータは、 とりあえず平均30で標準偏差5だと考えてみよう。 こうすると、たとえば第1試行での跳躍距離である30.5という観測値が、 平均30標準偏差5の正規分布から得られる確率は
となる。 (dnormの1番目の引数はx軸の値、 2・3番目の引数はそれぞれ正規分布の平均と標準偏差。) は非常に小さなxの幅であり、 これを確率密度にかけることで、確率を得ている(Figure 10a)。
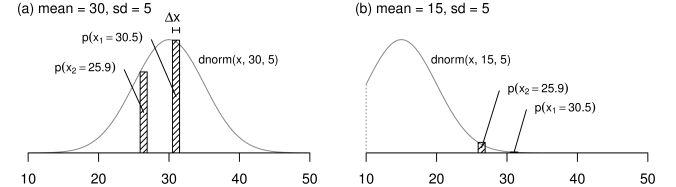
特定のパラメータ値を仮定した正規分布する母集団から およびという実観測値が得られる確率 (a) N(30, 52)を仮定した場合 (b) N(15, 52)を仮定した場合
どのみちはすぐあとで関係なくなるので、 「非常に小さな幅っていくつだよ」 といった心配はしなくてよい。
ともかく、 このようにデータを生みだした理論分布の形状とそのパラメータを仮定してしまえば、 各試行の実際の観測値が、 その分布からたまたま取り出される確率を計算することができる。 そして、 実際に得られたn試行分のデータの集合 がこの分布から得られる確率をLとおくと、 各試行の結果が独立とみなせば、
| (12) |
となる。 (は全要素の乗算を意味する。) Rのコードを交えると、
| (13) |
である。 いまは説明のため、分布のパラメータを30と5に固定した例を示したが、 一般化して書けば、 正規分布の平均を、標準偏差をと仮定したとき、 現実に得られたのと同じ観測値がその分布から得られる確率は、
| (14) |
となり、との関数となる。
ここで登場した左辺のLこそが、尤度である。 すなわち尤度は、ある理論分布を仮定したとき、 現実に得られた実データと同じ結果がその分布から生じる確率として定義される。 また尤度を理論分布のパラメータの関数として表わした上記の式を、 尤度関数と呼ぶ。 尤度関数は、仮定するパラメータの値と、 それに対する尤度の関係を記述する。 たとえば先と同様の例で、 正規分布のパラメータを平均15標準偏差5と仮定したとしよう(Figure 10b)。 この理論分布は15を中心に、5から25の範囲を95%区間として広がる分布である。 よってこのような分布を仮定した場合、 いまあなたが直面している現実(n試行分のカエルの跳躍距離の値)がここから生じる確率は、 非常に小さくなるだろう。 というのも、この分布にしたがえば、 30.5などという値が1回生じる確率でさえ非常に小さく、 そんな値がn回の試行で平均的に得られる可能性など、 ほとんど0といっていいからだ。
これが、尤度Lの値が仮定したパラメータに依存して変化するということの意味である。 つまりパラメータの値をいくつと設定するかによって、 その理論分布から現実事象と同じ結果がもたらされる確率の高さは変わる。 そして、パラメータの取り得るさまざまな値のなかから、 もっとも尤度が高くなるような値を見つけ出し、 それをパラメータの推定値とするのが最尤推定法である。 そのロジックは「現実に起こった事象をもっとも生じやすいようなパラメータこそ、 一番それらしい(尤もな)パラメータの推定値である」ということになる。
さて、ではどうやって尤度を最大化するようなパラメータをみつければよいだろうか。 尤度はEq.3.6で表わされるわけだから、 この関数の最大値を与えるパラメータ・を探せばよい。 注目したいのは、この関数が確率の積のかたちをとっていることだ。 このような大量の値の掛け算は非常に計算量が多く、 あとでRを用いた解析を行なううえでも問題となる。 そこでまず、この尤度関数において両辺対数をとり、
| (15) |
を考える。 これを対数尤度 log likelihoodという。 Rのコードを交えると
| (16) |
となる。 (dnormは、4番目の引数logをTRUEにすると、 確率密度の対数を返してくれる。 もちろんこれは、普通のdnormの返り値を log(dnorm(...))のように対数変換しても構わない。) 対数関数は単調増加な関数であるから、尤度Lの増減と対数尤度log(L)の増減は一致する。 すなわち、尤度を最大化するには、 この対数尤度を最大化すればよい。 また式後半のは定数だから、 尤度を最大化するパラメータを探すうえでは無関係である。 よって結局のところ、尤度を最大化するためには、Eq.16前半の
| (17) |
が最大になるようなパラメータおよびを探せばよいことになる。
では実際に、ある程度の幅でとを変化させたとき、 Eq.17の値がどうなるか、先のカエルの跳躍の例で調べてみよう。 Figure 11は、をx軸(横軸)、をy軸(奥行き)として、 そこから計算される対数尤度をz軸(高さ)にプロットしたものである。
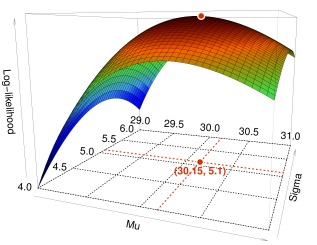
仮定するパラメータの値を、 を中心に段階的に変化させたとき、 が取る値
曲面の色はz軸の値の大きさにもとづいて塗り分けた。 われわれの目標は、尤度を最大化するようなパラメータをみつけることだから、 このグラフでいえば、 曲面の頂点にあたる部分のx座標()とy座標() の値を読み取ればよい。 この例では、、で対数尤度が最大になった。 すなわちこれらのパラメータの推定値が、 現実に起きた現象をもっとも引き起こしやすいということになる。 言い換えれば、、 がデータから得られた分布のパラメータの最尤推定値である。
このように、対数尤度を最大化するパラメータの値をさがすことで、 いまあなたが直面している現実を引き起こす確率がもっとも高い、 もっとももっともらしいパラメータの推定値を得ることができる。 しかし一般的には、このような尤度を最大化するパラメータ値を一意に探し出すのは、 それほど簡単ではない。 たとえば先の例では、標本の平均・標準偏差のごく周辺でだけパラメータを変化させて、 対数尤度が最大になるポイント(曲面の頂点)をさがした (Figure 11のx・y軸の範囲)。 しかしもっと離れたところから眺めたら、 じつはこの曲面は凹凸の激しい形状をしていて、 これよりも離れた所に、 対数尤度がもっと大きくなるような点が存在するかもしれないではないか。 もちろん、この例に限ってみれば、 これ以上正規分布のやを遠のけたとしても、 実データが得られる確率(尤度)が一転して高くなるということは考えづらい (Figure 10)。 しかし最尤法を用いたフィッティングでは、 (仮定した理論分布にもよるが)尤度関数がかなり複雑になる場合もある。 よって一般論として、 最尤法において尤度が最大となる点を解析的にもとめるのは不可能なことが多い。
このような理由により、対数尤度を最大化するパラメータ値の探索には、 一般に計算機による繰り返し演算が用いられる。 詳しい説明は省略するが、これは簡単にいえば、 パラメータをある値からはじめて少しずつ変化させ、 対数尤度がより大きくなったほうへとじりじり動かしていくような方法である。 これによって解析的に関数の最大値を調べることができない場合でも、 対数尤度を最大化するパラメータ(の有力候補) を効率的にみつけだすことができる。
まとめると、尤度とはある理論分布を仮定したとき、 実データとおなじ観測結果が得られる確率であり、 最尤推定法ではこの尤度を最大化するようなパラメータを推定値として採用する。 それは、現実に得られたデータをもっとも生み出しやすいパラメータこそ、 その事象が実際に起きたという現実に照らしあわせて、 いちばんもっともらしいからである。 このようなパラメータを解析的方法でみつけるのは困難であるが、 計算機をつかうことで、 現在では簡単に最尤法によるパラメータの推定を行なうことができる。
3.7 最尤法によるパラメータ推定
では、いよいよ実際にRで最尤推定をしてみよう。 と、意気込んだが、じつはやることはそれほど多くない。 先述のとおり、尤度関数を最大化するようなパラメータの探索はたいへんな仕事ではあるが、 それは計算機がやってくれるからだ。 われわれがやることは、最大化すべき尤度関数と実データ、 およびじりじり値を変化させてパラメータを推定するにあたっての初期値を、 Rの最尤推定関数であるoptimに渡すだけなのだ。
最尤推定の初期値には、モーメント統計量による推定で得た値を使えばよいだろう。 また解析対象のデータは、 当然だが自分の手のなかにある。 よってここでの実質的な作業としては、 尤度関数の定義ぐらいしかやることがない。 Code. 5.2のfitexGauss中盤で、 fnとして定義している関数である。 fitexGaussでは、 じつは3種類の方法でのフィッティングを採用しており、 最尤推定はそのうちデフォルトで使用される手法になっている。 これらの推定方法はfnのつくりかたのみが異なるので、 Code. 5.2ではfnの定義部分において条件分岐が入っている。 いまは最尤推定を意味するif (type == "ml")の分岐内で行なっている fnの定義に注目してほしい。 この関数は、ex-Gaussian分布の確率密度を dexGaussから対数化した状態で取り出し、 その和を返す。 まさにEq.15の式で表わしたそのまんまだ。 こうして定義した尤度関数を、 データxや初期値momfitと一緒に、 しかるべき形式でoptimに与えてやれば、 あとはRが最尤推定を行なってくれる。
ただし3つ注意点がある。 まず、これはoptimの仕様なのだが、 optimはデフォルトでは与えられたfnを (最大化ではなく)最小化するようなパラメータを探してくれる。 よってそのままでは、対数尤度を最小化する、 すなわち「もっとももっともらしくない」パラメータが推定されてしまう。 解決策は簡単で、尤度関数fnの定義において、 最終的な返り値の符号を反転してやればよい。 対数尤度のマイナスを最小化するということは、 対数尤度を最大化することと同義だからだ。 そのためfn内においては、 確率密度をsumしたのち、 最後にマイナス符号をつけて値を返している。
またoptimを用いて最尤推定する場合、 fnとして定義する尤度関数では、 推定してほしいパラメータを第一引数にベクトルとしてまとめて与える決まりになっている。 いまはex-Gaussian分布における・・を推定してほしいので、 尤度関数fnでは、 第一引数THETAと命名し、 これらのパラメータを上記の順で与えている。 fn内でdexGaussを呼び出す際、 THETA[1]をmu、 THETA[2]をsigma、 THETA[3]をtauとして与えていることからそのことがわかるだろう。 こうしたoptimの仕様について、詳細は
?optim
を参照されたい。
さらにこのTHETAについて、 fn内冒頭でexpをかけているのが不思議にみえると思う。 これは推定するパラメータを正の値に制限するための工夫だ。 ex-Gaussian分布は、 定義上とは正の実数でなければならない。 また時空がねじくれでもしない限り反応時間がマイナスの値を取ることはないので、 分布のピークを示すも当然正の値になるはずだ。 しかしこれはあくまでわれわれの特有の都合であって、 汎用関数であるoptimは、 正負さまざまな値にパラメータを動かしてfnを最適化する解を探しだそうとする。 よって与えるデータと初期値の質がたまたまよくないと、 optimがやをマイナスにした状態までも探索しにいってしまい、 エラーの原因となる。 (dexGaussの返り値がNaNやInfになるため。) これを避けるため、 fn内でまずTHETAの指数をとり、 パラメータが正の値しかとらないように制限している。 ただしこうすると、 optimが「この値が最適でしたよ」という答を出してきたとき、 実際にはその指数をとったものをdexGaussのパラメータとして使っていたということだから、 optimのあとで、 出力された推定値にもexpをかけ直すという作業をしている。
ともかくこれで主要な部分はできた。 あとは、推定計算時の警告出力の有無を切り替えたり、 最終的な返り値の書式を整えたりしてやれば、 fitexGaussの完成だ。 添付のプログラムでは optimによる推定計算以下にもコードが続いているが、 これは次項で説明するフィッティングのよさに関する解析を行なっている部分だ。 ex-Gaussian分布のフィッティングそのものについては、 optimまででおしまいである。 ちなみにfitexGaussは、実際の運用時の利便性のため、 「モーメント統計量による推定値」と「最尤法による推定値」だけでなく、 最尤推定におけるフィッティングの結果の詳細や、 プロット時に使用する元のデータの情報など、 さまざまな値を含んだリストを返り値として返す。 上記2種の方法によるパラメータの推定値は、 それぞれmom・loglikeと命名してあるので、 fitexGaussの返り値をなんらかの変数に代入し、 そこから$演算子などで要素取り出しをすればよい。
3.8 最尤推定における計算の収束
ここまで、反応時間データをex-Gaussian分布でフィッティングすることで、 データの分布上の性質を定量する方法を学んできた。 しかし、そのようにして得られたパラメータは、 実際のところどれぐらい信用できるのだろうか。 本項以降では、 推定計算の収束とデータに対する理論分布のフィッティングのよさを調べることで、 分布解析の妥当性を調べる方法を説明する。
と、ここで記憶のよいひとは、 「おいおい、最尤推定ってのは 『もっとももっともらしいパラメータを探してくる方法』なんだから、 それによって得られた推定値は必然的に一番よくデータと一致していて、 フィッティングがいいもわるいもないんじゃね?」とおもわれるだろう。 しかし、それは少々早合点だ。 そこには2つの問題が潜んでいる。 第一に、ここで扱う最尤推定は、単純な直線回帰などとは違い、 一意な解が解析的に必ず求められるという性質のものではない。 本来であれば人間が手計算で算出することなどできようもない値を、 コンピュータによる繰り返し計算によって、 ある意味無理やりに求めているのだ。 よって、最尤推定を実行したとしても、計算がうまくいかず、 最終的に得られたパラメータが必ずしも最良の値となっていないことがありうる。 さらに第二のポイントは、より根本的な問題として、 そもそもデータの分布が、 利用した理論分布の形状と全然違っているという可能性がある点だ。 反応時間の例でいえば、せっかくex-Gaussian分布でフィッティングしたのに、 そもそものデータが実は左に尾を引くような、負に歪んだ形をしていた、 といった状況である。 最尤推定はあくまで「その指定された理論分布でフィッティングするとすれば、 パラメータをこういう値にすると一番おさまりがいいよ」という値を探してくれる手法だ。 よって、そもそも想定した理論分布が実際のデータに即さないものであったとしたら、 推定されたパラメータは「その分布を敢えてあてはめるとすれば相対的に一番マシ」 というだけで、 絶対水準としてのフィッティング精度がよいとは言い難い。
このように、理論分布によってデータをフィッティングする場合、 上記の2つの観点からの「フィッティングのよさ」を検討しておく必要がある。 これはすなわち「その分布でフィッティングをすることの妥当性(適切さ)」の問題とも考えられる。 そこでこれらの点について、順に説明していこう99 最尤法における推定結果の妥当性に関しては、 この他に初期値の問題や極大への収束の問題などがあるが、 それらの網羅的解説は本稿の域を超えるためここではとりあげない。 詳細は数理統計学や計算機統計学の書籍などを参照されたい。。
まず第一点めの、最尤推定計算についてだ。 一般に最尤推定の計算は、パラメータの値を少しずつ変化させ、 それによって理論分布が実データに近づくようじりじり推定値を変化させるという、 繰り返し計算の過程を含んでいる。 これは、最尤推定が扱うフィッティング問題は概してパラメータ数が多く、 直線回帰のような「方程式を解いて最適解を導出する」 という方法がとれないためだった。 とはいえ最尤推定においても、 推定における基本ロジックは直線回帰と変わらない。 それは「適用したい分布と実データの一致具合を算出して、 それを最大化する」ということである。 データと理論分布の一致具合は、最尤法においては尤度で測られるのであった。 直線回帰であれば、 各データ点と回帰直線の距離があてはまり具合の指標となり、 その方程式を解くことで、 一番データに合致した直線の傾きと切片をもとめることになる。 直線回帰と最尤推定の違いはあくまで、 直線回帰なら一番あてはまりをよくする解が一意にもとまるが、 パラメータ数が多いとそうはいかない、ということだけだ。 そこで計算機を利用した最尤推定では、 現在の値から各パラメータをちょっとだけ変えてみて、 実データと理論分布のあてはまりがよくなったら、 それを新たな現在のパラメータ値とする。 この計算を繰り返すことで、尤度を上げるほうへ上げるほうへと、 じりじりパラメータを変化させていくのだ。 そして、パラメータの値をどう変えても尤度があがらなくなったところで 「尤度が最大になった」とみなし、 そのときの値が推定結果として返される。
以上が最尤法における推定計算の概要である。 このとき、パラメータが最適に至った結果、 尤度がそれ以上あがらなくなることを「計算が収束する」という。 逆にいえば、最尤推定の計算が収束したとき、 その推定結果は尤度の最大化の観点からもっともらしい値だといえるわけだ。 しかしこの最尤推定の計算は、時折、うまいこと収束しないことがある。 たとえばAとBというふたつのパラメータにおいて、 Aを大きくしてBを小さくしたときと、逆にAを小さくしてBを大きくしたときで、 どちらも同じくらい尤度が高くなるようなケースである。 この場合、 Aを大きくするか小さくするかの2パターンのあいだでパラメータの変動がいったりきたりを繰り返し、 結果として推定計算が収束しなくなる。
このように最尤推定が収束しなかった場合でも、 Rのoptim関数は「いちおうここまではたどり着きました」 というパラメータの推定値を返してくれる。 しかし計算の収束していないこの推定値には、 「パラメータをこの値にすれば尤度が最大化される」という保証はない。 よってこうした場合にはその推定値は使わず、 フィッティングに失敗したデータセット(たとえば実験協力者) として解析から除外するのが一般的である1010 あくまで少数のデータセットについて、推定が収束しない場合のはなし。 もし大半のデータで推定計算に失敗するのであれば、 それは初期値の設定やあてはめる理論分布など、 どこかべつのところに問題がある可能性が高い。 その場合には、単にデータを除外する以上の対処が必要である。。 fitexGauss関数の運用上でもこれは同様だ。 収束の成否を調べるには、 optim関数の返り値のなかのconvergence要素を参照すればよい。 convergence要素は、推定計算が収束した場合には0に、 収束しなかった場合には、ケースに応じた正の値となる。 よって各最尤推定計算ごとにconvergence要素を確認し、 それが0になっているデータセットだけを以降の解析に用いればよい。 fitexGaussは、 内部で行なったoptim関数の返り値をそのまま optimrslt要素として返してくれるので、 最終的には以下のような二重の取り出しで確認することになる。
x <- fitexGauss(rexGauss(100)) x$optimrslt$convergence == 0
ちなみにfitexGauss関数は、 これとまったく同じ値を、 自身が返すリストオブジェクトにも同名要素としてコピーするので、 同様の確認は
x$convergence == 0
とするだけでも行なうことができる。
3.9 フィッティングのよさの指標
次に、データに対するex-Gaussian分布のあてはめにおける、 フィッティングのよさの指標について説明しよう。
あらためて確認しておくと、 ex-Gaussian分布解析においてフィッティングのよさを調べることの意味は、 「そもそもそのデータにはex-Gaussian分布をあてはめるのが順当だったのか」 という問題と関連している。 最尤推定法は、指定された理論分布のパラメータをどういう値にすれば、 その分布を実データと一番うまく重ねられるかを教えてくれる。 しかしながらその理論分布が、 与えられたデータをフィッティングするのに適した分布だったのかについては、 無頓着である。 もちろんよっぽどデータの実状と合わない理論分布を指定したら、 前項で説明したように推定計算自体が失敗し、 計算が収束しなかったという「正しいエラー」が得られるだろう。 しかしたとえば、 本当は一様分布しているデータを正規分布でフィッティングしようとしたぐらいなら、 optim関数は尤度を最大化する正規分布のパラメータ (・)を教えてくれるだろう。 とはいえ実際のデータ分布が一様なのであれば、 平均まわりの値ほど出現率が高くなる正規分布でのフィッティングには、 おのずと限界がある。 データが一様にばらついているのであれば、 フィッティングには正規分布より一様分布を用いるべきなのだ。
こうした「その理論分布を用いるのはそもそも妥当か」という疑問に答えるためには、 実際その理論分布を用いたことで、 データをどの程度よくフィッティングできたのかを調べなければならない。 先の例であれば、データを正規分布でフィッティングしたとき、 そのあてはまり具合があまりよくなければ、 そもそも正規分布を用いたのが失敗だったと考えることができる。 また、正規分布と一様分布でそれぞれフィッティングしてみて、 そのあてはまりのよさを比較することにより、 どちらの理論分布がよりフィッティングに適しているかを調べることもできる。 まあ反応時間データに関していえば、 その分布がやや右に尾を引く釣鐘状なのはある程度既知なので、 「反応時間分布をex-Gaussian分布でフィッティングするか、 一様分布でフィッティングするか」といった比較が重要になることはないだろう。 しかしそれでも、絶対水準として ex-Gaussian分布がデータにどれだけ一致していたのかという検討はしておくべきだ。 そこで本項では、 分位点を利用して実データの分布と理論分布の類似性を調べる方法を解説する。
分位点 quantile (分位数、分位値)とは、 与えられたデータを値の大小に基づいていくつかのグループに等分したとき、 各グループ間の区切りとなる値である。 データをn個にわけるとすると、区切りの点はn-1個必要となり、 それらはn分位点と呼ばれる。 たとえばデータを大きさ順に4つのグループにわけるなら、 各グループの境となる3つの値が決まり、 それらを四̇分位点と呼ぶ。 注意したいのは、分位点がデータの範囲(最小値・最大値間の長さ)をn等分するのではなく、 データをn個の同じ観測数のサブグループにわけるということだ。 たとえば160人分の身長のデータがあったとすると、 おおざっぱにいえば、 背の順で下から40人目・80人目・120人目のひとの身長が四分位点となる1111 正確には背の順に40人ずつの4集団に分けたとき、 各集団の境となる値だから、 「40人目と41人目の身長の平均」のように、 小さいほうのグループのいちばん大きいひとと、 大きいほうのグループのいちばん小さいひとの平均値である。。
この分位点を、理論分布についてとることを考えてみよう。 連続的に変化する確率変数におけるデータの分布の仕方は、 定義域全体を積分すると面積が1となるような確率密度関数によって決められている。 これを同じ大きさのn個の集団にわけるということは、 密度関数を下から順に積分していって、 面積が1/nになる点ごとにデータを区切っていくのとおなじである。 たとえば正規分布における四分位点なら、 正規分布の密度関数の下側面積を1/4ずつにわける区切りの3点となる(Figure 12a)。
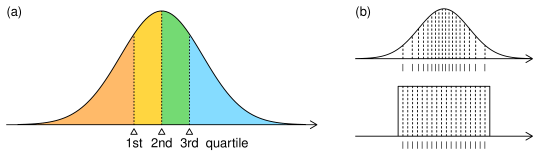
(a) 正規分布における四分位点。 各色の面積はすべておなじ0.25で、 分布全体をこれらの4群にわける3つの点の値が四分位点 (b) 分布間での分位点の違い。 正規分布(上段)では平均値周辺における確率密度の高まりを反映し、 面積を等分する点の間隔は狭くなる。 一様分布(下段)では定義域全域で確率密度が一定なため、 分位点間の間隔も一定となる。
数学的に定義された分布の分位点は確率点と呼ぶことも多いが、 その場合も指しているものは一緒である。 四分位点はデータを25%ずつに分割するから、 25・50・75%確率点ということになる。
ではこの分位点を、異なる理論分布間で比較してみよう。 Figure 12bに、 正規分布(上段)と一様分布(下段)においてそれぞれ二十分位点をとった例を示した。 両分布において、点線で区切られた各小領域の面積は等しく1/20で、 そのときの分位点が分布の下にバーコード状に表示してある。 一見してわかるとおり、一様分布は分位点間の間隔が均一なのに対し、 正規分布では中央に寄った分布をしている。 これは正規分布の確率密度関数が平均値周辺ほど高くなっており、 面積を一定にするために必要なx軸方向の幅が、 そのぶん小さくて済むためである。 このように、分位点は確率密度関数の下側面積を等分に分割するため、 確率密度が高いところでは間隔が密に、 逆に低いところでは間隔が疎になる。 言い換えれば、理論分布からn分位点を計算することは、 その分布の密度関数がもつ確率密度の増減の特徴を、 n-1個の分位点の粗密の情報に変換するのと同義である。
そこで、実データと理論分布の一致の具合を調べるために、 分位点のこの性質を利用する。 たとえばあなたが、64試行分の反応時間のデータに対し、 ex-Gaussian分布のフィッティングを行なったとする。 ヒストグラムとの重なりのよさをみれば、 このデータにex-Gaussian分布をあてはめるのは妥当に思える(Figure 13a)。
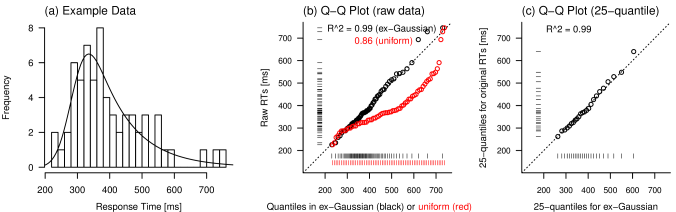
(a) 64試行分の擬似データとex-Gaussian分布のフィッティング結果 (b) 全データ点を用いたQ-Qプロット (c) データおよび理論分布の五十分位点を用いたQ-Qプロット
しかしどうすればそれを定量できるだろうか? ネックになっているのは、手持ちの「64個の数値」という点データが、 「確率密度分布」という数式で規定される理論分布の形状と直接比較できないことである。 だったら、直接比較できるよう、 理論分布を実データと同数の数値列に変換してやればよかろう。 すなわち、フィッティングの結果得られたex-Gaussian分布から、 64個の分位点をつくってやればよいのだ。 n分位点はn-1個あるわけだから、64個の分位点を得るには、 理論分布を65等分した六十五分位点をとってやればよい。
おさらいだが、この六十五分位点は、 指定したパラメータをもつex-Gaussian分布の確率密度情報を、 64個の分位点の粗密として表現したものと考えることができる。 そこで、こうして得られた分位点の値を横軸にとり、 昇順にならべた実際のデータ点を縦軸方向にプロットしたのが、 Figure 13bのグラフにおける黒色の点である。 理論分布から生成した分位点(x軸に沿った黒のバーコード模様)は、 200強から開始して750前後まで、 なめらかな粗密によってex-Gaussianの右に尾をひく分布形状を表わしている。 一方実際のデータの昇順列(y軸に沿ったバーコード模様) はそれよりも粗密が乱れているが、 やはり350あたりを頂点として、 200から750まで広がる正に歪んだ分布をしている。 よってこれらの値を小さいほうから順番にx・y座標として打ったプロット点は、 傾き1の対角線上におよそ整列しており、 x座標値とy座標値の強い相関を示している。 実際、このグラフを直線回帰すると、 決定係数 coefficient of determination (で表わす)は0.99と非常に高い値になる。 決定係数は、 独立変数が従属変数のもつばらつきをどの程度説明できるかを表わす指標だから、 ここでは理論分布(からつくった分位点) と実データの分布がほとんど一致したことを意味する。 すなわち、このデータに対する ex-Gaussian分布のフィッティング精度は非常によかったと考えることができる。
ではたとえば、同じ擬似データに対して異なる理論分布を適用するとどうなるだろう。 試しに、実データと同じ範囲を定義域とする一様分布から分位点を生成し、 同様のプロットをしてみたのがFigure 13bの赤のドットである。 一見してわかるように、できあがったグラフは対角線よりもかなり下にズレていて、 計算される決定係数も0.86と、 ex-Gaussian分布での結果を大きく下回っている。 これは、一様分布からつくりだした分位点 (x軸に沿った赤のバーコード模様)が定義域全体を均等にカバーするため、 実際のデータではほとんどみられない大きな値の点が多数含まれてしまったからである。
このように、理論分布からつくりだした分位点と実際のデータ点を散布図としてプロットし、 その決定系数を計算することによって、 データに対する理論分布のあてはまりのよさを定量することができる。 fitexGauss関数は、フィッティングの実行ごとにこの値を算出し、 返り値のr.squared要素として返す。 よってそれをすべてのフィッティングに関して何らかの変数に格納しておき、 全体平均として高い値となっていることを示せれば、 使用した反応時間データがex-Gaussian分布のあてはめに適したものだったと主張できるだろう。
x <- fitexGauss(rexGauss(100)) x$r.squared
ただしここで計算される決定係数は、 一般的な実験データなどに直線回帰をしたときよりもかなり高い値となるので、 その点には注意が必要だ。 これは計算の手続き上、 x座標の分位点とy座標の昇順化したデータ値がいずれも単調増加になるため、 すべての点間において右肩上がりの推移が保証されているせいである。 散布図上ではあきらかに対角線から逸脱した Figure 13bの一様分布のプロットでさえ、 決定係数は0.86と、 一般的にいえばかなり高い値となっていることからも、 そのことがわかるだろう。 経験的にいえば、よく成功しているex-Gaussian分布のフィッティングでは、 決定係数は0.95より大きくなることがほとんどであり、 0.9を下回るようなことはまれである。 逆にいえば、そのような相対的に低い決定系数値が得られたら、 実際のデータやヒストグラムとあわせて検討し、 必要であればそのデータセットは解析から除外する等の処置が必要だろう。
ちなみに実際の運用においては、使用するデータ数が多い場合、 生データの点をすべて用いるのでなく、 データと理論分布からそれぞれn分位点を計算し、 分位点同士の散布図の相関をみる場合も多い。 たとえばFigure 13cは、 Figure 13bと同じ擬似データについて、 データと理論分布から取り出した二十五分位点をもとに再計算したものである1212 実際には、100個未満程度の少数のデータに関して、 わざわざ二十五分位点なんぞを取り直して決定系数を計算することはまずない。 しかしたとえば、実験データについて不要な要因を潰してひとまとめにしたため、 1回のフィッティングに使うデータのサンプルサイズが数百や数千試行分などになった場合、 百分位点を用いた決定系数の算出などを利用することがある。。 分位点(q̇uantile)同士をプロットすることから、 このような図をQ-Qプロットと呼ぶ。 データから計算した分位点を用いたQ-Qプロット(Figure 13c)においても、 元のデータをそのまま用いたQ-Qプロット(Figure 13b) とよく似た散布図や決定系数値が得られていることがわかる。
3.10 データと理論分布の一致性の検定
前項において理論分布から分位点をつくりだしたとき、 「値としてのデータ点と数式としての理論分布形状を直接比較できないのがネック」だと書いた。 しかし実は、コルモゴロフ-スミルノフ検定 Kolmogorov-Smirnov test(KS test)を用いれば、 そのような比較を直接することも可能である。 2標本コルモゴロフ-スミルノフ検定は2つのデータセットの分布形状を比較する検定手法だが、 1標本コルモゴロフ-スミルノフ検定は、 任意の理論分布と標本分布の一致性を検定できる。 Rにおいてはks.test関数を利用すればよい。
方法としては、フィッティングに用いた実データを経験分布としてks.testに与え、 比較する相手として最尤推定されたパラメータ値をもつex-Gaussian分布の累積密度関数を指定する。 コルモゴロフ-スミルノフ検定の帰無仮説は「与えられたふたつの分布形状が等しい」なので、 検定の結果p値が0.05より小さくなった場合、 データの分布が理論分布とおなじとはみなせないことを意味する。 指定する密度関数には最尤法で推定されたパラメータをつかっている以上、 ex-Gaussian分布を使用する場合の最良のフィッティングが得られているはずなのだが、 それでもなおデータと理論分布が食い違った。 だとすればそのデータは、 そもそもがex-Gaussian分布でフィッティングするべきものではなかったと考えられる。
fitexGauss関数は、フィッティングの実行時にこの検定も自動で行ない、 その結果をksrslt要素として返す。 単純にそれをRターミナル上でprintすれば、 検定の結果が表示される。 またksrslt要素内のp.value要素を参照することで、 p値の取り出しも可能である。
x <- fitexGauss(rexGauss(100)) x$ksrslt x$ksrslt$p.value
ここまで数項にわたり、 ex-Gaussian分布を利用した反応時間解析において、 フィッティングの精度を調べる方法について説明してきた。 最後に、フィッティングがうまくいった場合とそうでない場合において、 とりあげた指標がどのような値になるか、 Figure 14に一例を示す。
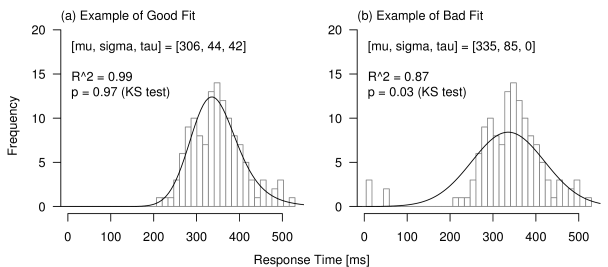
ex-Gaussian状の分布形状をもっていたとしても(a)、 少数のハズレ値の存在により(b) フィッティングの精度が低下する例。 Q-Qプロットの決定係数やKS検定の結果を参照することで、 (b)のようなケースを除外することができる。
どちらの擬似データに関しても、一応fitexGaussによる最尤推定は収束し、 推定されたパラメータに基づくex-Gaussian分布がヒストグラムと併記されている。 しかしながら(b)の例では、 少数存在する非常に小さな値に引っ張られてが0となり、 実質的に正規分布でフィッティングされた状態となっている。 ヒストグラムをみても、明らかに理論分布との食い違いが大きい。 そこで両フィッティングについて、 Q-Qプロットにおける決定係数とコルモゴロフ-スミルノフ検定の結果をみてみよう。 (a)のデータでは決定係数が0.99と非常に高く、 コルモゴロフ-スミルノフ検定の結果、 理論分布と実データ間の有意な分布形状の違いもみられない。 一方(b)のデータでは、決定係数が0.87と低く、 しかも検定により有意な分布形状の差が認められている()。
以上のように、これらの指標を用いると、 その理論分布を用いてデータをフィッティングしたことの良し悪しを調べることができる。 実際の運用例としては、 たとえば、 各フィッティングについてまずコルモゴロフ-スミルノフ検定の結果を参照し、 有意差がみられたデータセットについては解析から除外する。 そのうえで残りのデータに関して、 Q-Qプロットの決定係数の平均値などを提示して、 データに対するex-Gaussian分布がのあてはまりがよいことを示すとよいだろう。
3.11 実習
さて、いよいよ本解説文も大詰めだ。 ex-Gaussian分布を用いた反応時間解析の説明の最後として、 本項では、より実践的なデータ解析の実習を行なう。 データの読み込み・ex-Gaussian分布解析・グラフ化という一連の作業を追うことで、 実用的なツールとしてこの解析方法を身につけてもらいたい。 またCode. 5.4に解析全体の例を載せておいたので、 参考にしてほしい。
実習をはじめるにあたり、まず解析する対象となる擬似データをつくる必要がある。 第3.1項でのようにrexGauss で反応時間データだけつくりだしても構わないのだが、 より現実の解析場面に近い状況のほうが、実習の意義も大きいだろう。 そこでここでは、 実験結果の記録されたテキストファイルのかたちで擬似データを生成し、 それを読みだすところから解析の練習をはじめたいと思う。 リンクからhttp://noucobi.com/Rsource/exampleRT.Rを保存し、 R上で実行してほしい。
source("exampleRT.R")
これにより、現在のディレクトリにdataというフォルダがつくられ、そのなかに 15人分の擬似データが生成される。
できたファイルのひとつを、 試しにワードパッドなどのテキストエディタで開いてみよう1313 自身の名誉のために書き置くと、 筆者はLinuxユーザなので 「テキストエディタの代表=ワードパッド」などとはゆめ思わないのだが、 想定される読者のレドモンド率の高さを考慮してこのような言い回しとなっている。。 この擬似データファイルは、実験協力者に300試行からなるStroop課題を行なってもらい、 各試行での課題条件や反応時間、反応の正誤などを記録したもの、という想定でつくられている。 Stroop課題はあまりにも有名なので、わざわざ説明する必要もないだろう。 ここではStroop課題のなかでももっとも単純な課題構成を想定した。 画面上に現われる単語は「red」「green」「xxx」「xxxxx」の4種類であり、 文字の色は「赤」「緑」の2種類だけである。 文字が色と一致していれば「一致congruent」、異なるなら「不一致incongruent」、 文字が「xxx」ないし「xxxxx」ならば「中立neutral」な試行とする。 3つの課題条件はそれぞれ100試行ずつ、計300試行がランダムな順で呈示され、 協力者の課題は、なるべく早く呈示された刺激の色を答えることである。
生成してもらった擬似データのテキストファイルには、実験協力者ごとに、 各試行での「文字word」「色color」「条件cond」「反応時間RT」「正誤cor」の情報が記録されている。 正誤の欄が1なら、協力者がその試行で刺激の (印字の)色を正しく命名できたことを意味する。 一般に協力者の音声反応の正誤を自動で判別するのは難しいので、 この正誤の欄は、 実験中に実験者であるあなたが耳で聞いて判断し、 あとからこのファイル上に入力したもの、 ということにしよう。 ただし反応時間のデータは、 録音された音声信号の立ち上がりを自動判別して記録したもので、 客観性・信頼性ともに問題はないとする。 (実際のStroop課題の実験でも、このような実験デザインをとることが多い。 それから念のため繰り返しておくが、この実習で扱うデータは、 Rでそれらしく生成した擬似データである。)
さあそれでは、とりあえず1人分のデータを使って、反応時間解析を行なってみよう。 まずはデータの読み出しである。 データファイルをみると、はじめの3行は実験に関する一般的な情報が載っていて、 さらに空行を1行はさみ、データ部分が始まっている。 データ領域の最初の行には各列の名前(ヘッダ)が記入され、 行内はタブ区切りにされている。 よってデータの読み出しは、
tmp <- read.table("./data/sub_1.txt",
header=TRUE, skip=4)
のようにすればよい。 これで実験協力者1のデータが取り出せた。
実験のつくりにもよるが、一般に反応時間の検討を行なううえでは、 実験協力者が正しい反応をした試行だけを用いる。 もちろん、正答試行と誤答試行での反応時間の比較といった解析もありうるわけだが、 ここではとりあえず、もっともオーソドックスな正答試行の反応時間解析に焦点を絞ろう。 さきほど取り出したデータのうち、 正答試行の情報だけを別のデータフレームに取り出す作業は
cor <- tmp[as.logical(tmp[, "cor"]),]
によって実現できる。
さらに、これらを試行条件ごとのデータに分ける必要がある。 これは、データのcond列を参照すればよい。 今回の実習ではどのみち反応時間のデータしか使わないので、 データフレーム全体ではなく、 RT列だけを取り出したうえで条件ごとに分離しておこう。
cond <- cor[, "cond"] RT <- cor[, "RT"] RT <- split(RT, cond)
これでRTは、各条件における正答試行の反応時間データを要素としてもつ、 長さ3のリストとなった。
あとは簡単。 条件で分類したデータを
fitexGauss(RT$cng) fitexGauss(RT$neut) fitexGauss(RT$incng)
のようにfitexGaussに渡してやれば、 先述のとおりex-Gaussian分布でのフィッティングが行なわれ、 条件ごとに推定されたパラメータが返される。 ついでなので、一般的な要約統計量として平均値と標準偏差も求めてみよう。
sapply(X=RT, FUN=mean) sapply(X=RT, FUN=sd)
以上がひとりの実験協力者に関する、解析の結果となる。
このようにフィッティングを用いた反応時間分布解析では、 通常は各実験協力者について、条件ごとのフィッティングをそれぞれ行ない、 パラメータの推定値を得る。 いまの例では、試行条件は3種(一致・中性・不一致)、 統計量は5種類(平均値・標準偏差・・・)で、 実験協力者は15名なので、全協力者について上記と同様の解析を行なうと、 その結果はの配列に格納できる。 それが、Code. 5.4におけるrsltである。 そのうえで一般的な研究では、 これらの推定値について条件間での比較を行なう。 この例でいえば、各指標に関して対応のある一元配置分散分析(乱塊法)を実施し、 有意な差が見られれば、下位検定を行なう。 サンプルコードでは、statRTという関数により、 とりあえず分散分析とTukeyのHSD法による下位検定のみを行なうようにした。 しかし当然ながら、パラメトリックな統計手法の適用においては、 事前にデータの正規性や等分散性の検討がなされなければならない。 必要に応じた統計検定を追加してほしい。
Figure 15は、この擬似データの解析結果を要約したグラフである。
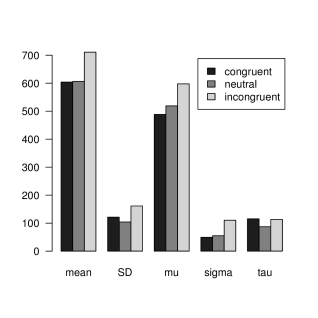
横軸は統計量の名前、縦軸はその値を示す。
練習のため、この結果の解釈をしてみよう。 まずグラフの左2種の指標、平均値と標準偏差についてみてみる。 これらはデータの数値要約において、もっともひろく用いられている指標である。 グラフをみると、なによりまず不一致条件における平均反応時間の増加が目に付く。 これは不一致条件において、 呈示された文字と色の食い違いが引き起こした干渉効果だと考えられる。 一方、一致条件と中立条件を比べると、 一致条件において若干の標準偏差の増加がみられるものの、 平均反応時間にはほとんど差がないようだ。 この結果に基づけば、呈示された刺激の色の命名においては、 文字が刺激の色と同じものであろうがxxxのような無意味なものであろうが、 反応における差異はないと結論できるだろう。
しかし、グラフの右側3種、 ex-Gaussian分布のフィッティングで得られたパラメータに注目すると、 はなしは変わってくる。 こちらのグラフをみると、一致条件は中立条件と比べ、 パラメータ(正規分布部分のピーク)の値は減少しているのだが、 一方での値は増加していることがわかる。 すなわち一致条件は中立条件と比較して、 反応時間の分布のピークは全体に小さいほうへとシフトするものの、 分布の尾も右へ長く引くようになっていたわけだ。 これは一致条件の文字刺激が、 自動的な意味判断を引き起こして処理量を増加させる負荷としての効果と、 その文字の意味が色と一致することによる促通としての効果という、 ふたつの性質をあわせもっているためと推測できる。 もちろん、これはあくまで推測にすぎない。 しかし少なくとも、一致・中立条件間で平均反応時間に差がみられなかったのは、 とに独立に生じた影響が相殺したためであり、 このふたつの条件が質的に異なるものであることは明らかだ。





 @kanri_ninjin
@kanri_ninjin



 イクナイ! 581
イクナイ! 581