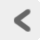2 分布のフィッティングによる反応時間データの解析
前節でみたとおり、 心理学実験によって得られる反応時間データは正に歪曲していることが多く、 単一の代表値を用いた解析では分布の特徴を適切に表現することはできない。 とくに、右に長く引いた分布の尾の成分は、 課題・環境・協力者などが異なるさまざまな実験においてひろくみられる特徴であり、 反応時間というデータ形式に特有の情報を含んでいる可能性がある。 このようなデータを正しく解釈するために、 少なくとも「ピークの位置」と「尾の引き方」というふたつの特徴は、 それぞれ別の指標によって定量化する必要がありそうだ。
本節では、反応時間分布と類似した形状をもつ理論分布を用い、 理論分布でのフィッティングから推定されたパラメータによって、 反応時間データの分布特徴を定量する方法を説明する。 まず前半では、フィッティングによる解析一般に関する解説を行なう。 そして後半では、 われわれの目的に使えそうないくつかの理論分布の候補のうち、 とくにex-Gaussian分布を用いた解析手法をとりあげ、 その方法を詳しく説明する。
2.1 分布のフィッティングによる解析
フィッティングによる反応時間解析の説明を始めるにあたり、 本項では、 まずそもそもフィッティングとはなにか、 フィッティングによってどんなことが分かるのかということを簡単に説明しておこう。
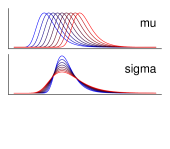
実験により得られたデータを「フィッティングする」といった場合、 くだいていえば、 それは「既知の理論分布が実データともっともよく重なるようにパラメータを合わせる」 ことを意味する。 ここで理論分布とは、数学的な式で定義されている分布だと考えればよい。 いまはフィッティングしたい対象が反応時間データのヒストグラム、 すなわちどのぐらいの値(横軸)がどれほどの頻度(縦軸)で観察されたかという頻度データである。 よって理論分布としても、 それぞれの値(横軸)がどの程度の割合(縦軸) で生起するかを示す確率密度分布(離散データなら確率分布)を使うのが適切である。 確率密度分布にはさまざまなものがあるが、 いちばん有名なのは正規分布 Normal distribution (ガウス分布 Gaussian distribution)だろう。 正規分布はFigure 5aのような釣鐘状の分布で、 とというふたつのパラメータをもつ。
(a) の正規分布(標準正規分布) (b) を1に固定し、の値を動かしたときの分布の変化 (c) を0に固定し、の値を動かしたときの分布の変化 (青いほどそのパラメータの値が小さく、赤いほど値が大きいことを示す。)
ここでパラメータ parameter(母数) とは分布の形状を変化させる数式内の定数のことだ。 同じ正規分布であっても、パラメータの値が異なれば分布の形状も異なる。 数理統計が嫌いではない読者のために載せておくと、正規分布の確率密度関数は
| (2) |
と表わされ、式のなかに表われているとには、 それぞれ具体的なひとつずつの値が入る。 そのうえでのさまざまな値に関して、 それが得られる確率の密度を示したものがこの式ということになる22 統計学が苦手な方は、「確率密度とはなんぞや」は難しく考えず、 確率のことだと読み替えてもらって構わない。。 左辺のカッコ内における縦棒より右側のとは、 「この分布はこんなパラメータをもっていますよ」ということを、 明示的に分かりやすく書いているだけにすぎない。 正規分布のふたつのパラメータとは、 それぞれ分布におけるピークの位置と裾野のひろがり具合を示しており、 の値が大きいほどピークの位置が右に、 またの値が大きいほど分布のひろがりがなだらかになる (Figure 5b・c)。
このように数式によって定義され、 パラメータに依存して分布の形状を変化させる理論分布を用いて、 実験で得られたデータをフィッティングすると、 どんな良いことがあるのだろうか。 例をつかって説明しよう。 いま、何らかの実験により、 Figure 6aのヒストグラムのようなデータを得たとする。
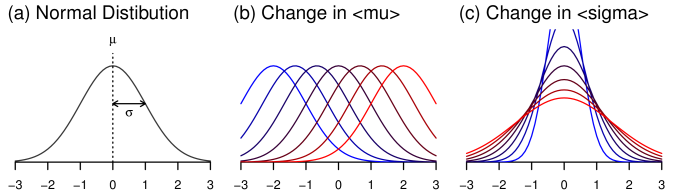
(a) 双峰性の分布をもつデータの例。 右上はフィッティングにより得られた理論分布のパラメータ (b) 2つの正規分布の合成からなる理論分布
実験はべつに何でもよいのだが、 たとえば近くの小川でカエルを捕獲して体長を測ったということにしよう。 すなわちFigure 6aは、横軸でカエルの体長(cm)を、 縦軸で捕獲されたその体長の個体の数を表わしていることとする。 一見して分かるように、このデータは双峰性の分布をとっており、 調査したサンプルのなかに2種類の異なる種が存在したことが推測される33 小さめのほうをシュレーゲルアオガエル、大きめのほうをウシガエルと 考えると、数値的にもFigure 6aのヒストグラムと符合する。 (ウシガエルはもう少し大きなものもみられる。) ちなみにシュレーゲルアオガエルは日本の固有種であり、 一方のウシガエルは固有生態系を破壊する悪名高い特定外来生物である。 よってこの戦いは、日本を蛮族の侵攻から守る戦いでもある。 44 それにしても調査時にシュレーゲルアオガエルとウシガエルの区別もつけず、 同じ「カエル」として体長だけ測るとは、いったいどういうつもりなのか。 。
さて、このようなやや複雑な分布をもつデータを、 いったいどのように解析すればよいだろうか。 明らかに、このデータに関して「とりあえず平均値をとる」というのは、 まったくの無駄とはいわないまでも、あまり有効ではなさそうだ。 なぜなら、このような双峰性のデータを平均化すれば、 大きな観測値と小さな観測値が相殺しあい、結果、 実際にはそれほど多く観察されていない中程度の値(7–8cm) が全体の「代表値」ということになってしまうからだ。 かといってヒストグラムをみながら2つのグループの境を恣意的に決め、 大小それぞれのグループごとに平均値を算出するというのも、客観性に欠ける。
このようなデータについて、 ある程度の客観性をもって分布の特徴を定量化するための方法が、 フィッティングによる解析だ。 先述のとおり、フィッティングによってデータを定量するためには、 フィッティングする相手としての理論分布が必要不可欠である。 ここではヒストグラムの特徴から、理論分布として、 ふたつの正規分布を合成してできた双峰性の分布を使うことにしよう (Figure 6b点線)。 ひとつの正規分布はとという2つのパラメータをもつから、 この分布は両方の山のピーク位置・ およびそれぞれの裾野のひろがり・ という計4つのパラメータをもつことになる。 これらのパラメータはそれぞれ独立に変化させることができ、 それに応じて分布の形状が変化する。
この分布を用い、実際のデータと理論分布がもっとも重なるようにパラメータを調整すると、 Figure 6aの点線のようになる。 一見して、この理論分布は実データのヒストグラムと非常によい一致をしていることが分かる。 そしてこのようなもっともよいフィッティングを与えたときの理論分布のパラメータの値をみることにより、 分布の特徴が定量化される。 Figure 6aの例では、理論分布における4つのパラメータは、 フィッティングの結果、グラフ右上に記された値となった。 2つのの値は分布の2つのピークと一致し、またの値から、 大きいほうのグループのほうが体長のばらつきが激しいということも、 きちんと定量されていることが分かる。
このように数学的に定義された理論分布でデータをフィッティングすることで、 理論分布のパラメータの推定値というかたちで、 データの特徴を定量することができる。 いまは反応時間における頻度データの解析を目標としているので、 確率密度分布を用いた例を紹介した。 しかし回帰分析における回帰係数や切片の算出なども、 理論分布のパラメータの推定値としてデータを定量するという意味ではまったくおなじである。
さてここで、たいへん重要な部分に関する説明が抜け落ちているのにお気づきだろうか。 それは「いったい何をもって『フィッティングのよさ』を決めるのか」、 すなわち「どうやってデータともっとも一致する理論分布のパラメータをみつけだしたのか」 ということである。 たしかにFigure 6aの点線は、 ヒストグラムとよく重なっているようにみえる。 しかしいずれかのパラメータをもうちょっとだけ変化させたほうが、 実データと理論分布がよりよく重なることはないのだろうか。 どうやってそれがないと保証されるのだろうか。
じつはこの部分の計算アルゴリズムは非常にややこしく、 またフィッティングする対象となるデータの質に依存して、 さまざまな異なる方法がある。 しかし、そのような計算過程の詳細を逐一並べたて、 本来ならいますぐにでも自分のデータを解析したい読者諸氏の心を折るのは、 本解説文の目的にそぐわない。 そこで本文書では、 フィッティングの最適化にともなう計算過程の詳細には立ち入らないことにする。 ただ一般論としては、このような複雑な分布によるフィッティングの過程も、 単純な線形回帰と同様、理論分布と実データとの「距離=食い違いの程度」 を最小化するものである。 ただその「距離の最小化」が一意の解の導出で達成できる線形回帰と違い、 理論分布が複雑な場合では、 計算機によって理論分布のパラメータを少しずつ変化させ、 そのつど実データと理論分布の距離を算出しながら、 より距離が縮まる値へとパラメータを動かしていく繰り返し計算の過程が必要になる。 そう書くとややこしく聞こえるかもしれないが、 Rを用いて計算させれば、 フィッティングそのものはたった1行で済むので恐れる必要はない。 そのような実際の解析の手順については、第3節で扱おう。
ちょっとごたごたしたが、とりあえず本項では、 フィッティングによる解析とは何なのか、 それによってどのようなかたちでデータを記述することができるのかを説明した。 重要なことは、理論分布によってデータをフィッティングすることで、 その分布のパラメータの推定値として分布の特徴を定量化できるということだ。 また同時に、このような解析のためには、 フィッティングの相手としてどんな理論分布を用いればデータをうまく定量できそうか、 という事前の見通しが必要ということも重要だ。 本項の例では、 ヒストグラムの形状の観察に基づき、 2つの正規分布を合成した分布を使ってデータをフィッティングした。 しかしわれわれの目的は、反応時間データの分布特徴を解析することである。 第1節でみてきたような正に歪んだ分布をとるデータは、 いったいどのような理論分布でフィッティングするのかよいのだろうか。 次項では、反応時間解析において用いられるいくつかの理論分布を紹介しよう。
2.2 反応時間解析に使われる分布
本項では、反応時間データのフィッティングに用いられる理論分布を紹介する。
おさらいすると、 反応時間データは正規分布に似た釣鐘状の形状をもつが、分布が右に尾をひき、 正に歪曲していることが特徴だった。 よってそのフィッティングには、正規分布のような左右対称の理論分布ではなく、 歪曲を表現できるような分布を用いる必要がある。 本項では、反応時間のフィッティングに利用できそうな正に歪んだ形状をもつ理論分布のうち、 比較的単純なものをいくつか紹介する。 ただし、これらの理論分布は、 いずれも単に「経験的な反応時間分布と類似した正の歪みをもつ」 という理由においてフィッティングに用いられるものである。 すなわちどの理論分布に関しても、 フィッティングに「その分布を使わなければならない」という理論的根拠は、 ほとんどの場合存在しない。 フィッティングの精度という意味では、 ここで紹介するどの分布を用いても、 実際の反応時間データをそれなりによくフィッティングすることができるだろう。 また本項では各理論分布の特徴やその確率密度関数などを紹介するが、 べつに反応時間解析をするためにこれらすべての分布を逐一理解する必要はまったくない。 あくまで知的好奇心というレベルで、 「こんな分布があるのか」と思いながら読み流してもらえれば充分だ。
Table 1に本項で紹介する理論分布をまとめた。
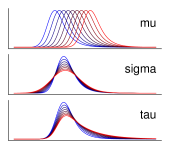
| (a) ex-Gaussian | ||||||||||
|
|
|
|
||||||||
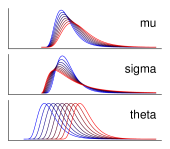
| (b) shifted Lognormal | ||||||||||
|
|
|
|
||||||||
| (c) shifted Wald | ||||||||||
|
|
|
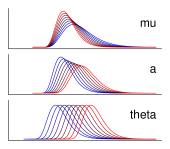
|
||||||||
| (d) shifted Weibull | ||||||||||
|
|

|
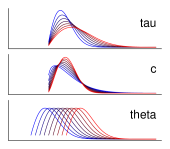
|
||||||||
| (e) Gumbel | ||||||||||
|
|
|
|
1列目は各分布の確率密度関数、 2列目は適当なパラメータ値で生成した分布の一例、 3列目は各パラメータについて、 他のパラメータ値は固定して段階的に変化させたときの分布の変化を示す。 青色ほどそのパラメータ値を小さく、 赤色ほど大きくした際の分布形状を示している。 (a) ex-Gaussian分布 (b) shifted Lognormal分布 (c) shifted Wald分布 (d) shifted Weibull分布 (e) Gumbel分布
各行がそれぞれ異なる理論分布を示しており、 1列目に分布の名前と確率密度関数、 2列目に分布の形状の例、 3列目に各パラメータを変化させたときの分布の形状の変化を示した。 2列目の代表例は、 いずれの分布も平均300、標準偏差60程度になるよう適当にパラメータを調整した。 一見して、どの分布も実際の反応時間データに類似した正の歪曲をもっていることがわかる。 気になるひとへのサービスとして、表中にはすべての分布の確率密度関数も載せているが、 べつにこれをみてうんざりすることはない。 どのみち本文書においては、 これらの分布の数学的定義に立ち入った説明はほとんど行なわないから、 安心してほしい。
それでは各分布、順を追って簡単に説明していこう。 1つめの分布はex-Gaussian分布 である(Table 1a)。 ex-Gaussian分布は、正規分布(Gaussian)と指数分布(exponential)の足し合わせによって できる分布である55 すでにex-Gaussian分布をご存知の諸兄には気に障る表現だろうが、 ここでは簡単のため、あえて数学的には正確でない書き方をしている。 ex-Gaussian分布のより正確な定義については、 次の第2.3項でもう少し踏み込んで説明する。。 数学的には正規分布と指数分布の 畳み込み convolutionという。 そのこころは単純で、正規分布は反応時間データに似た釣鐘状の形状をもつが、 左右対称なところがそれっぽくないので、 右に尾を引く指数分布を足してやることで歪曲の部分を演出しようというものだ (Figure 766 この図もやはり誤解をまねきかねないものではあるが、 直感的理解を優先するためにお目こぼし願いたい。)。
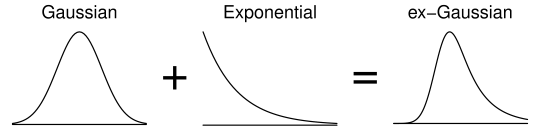
ex-Gaussian分布は・・という3つのパラメータをもつ。 これらのパラメータは、 もとの正規分布と指数分布からそのまま引き継いだものである。 すなわち、 とはex-Gaussian分布における正規分布様の部分のピーク位置とその広がりを示しており、 は指数分布部分の平均、すなわち尾の引き方の長さを決定する。 古典的な反応時間分布の解析では、 このような正規分布と指数分布を足し合わせた分布の特徴は、 反応の実現において必要とされる 「認知的な判断」と「運動の実行」 という2つのステップにかかる時間と結びつけて議論されていた。 この議論においては、 1回1回の反応にかかる時間のばらつきは、 その反応を行なうという認知的判断をする過程のゆらぎと、 実際にその運動を行なう運動過程のゆらぎの二者によってもたらされ、 前者は指数分布するのに対して後者は正規分布すると主張された。 すなわち、運動実行の過程は一定の平均を基準に早かったり遅かったりし(正規分布)、 一方であたまのなかでの判断の過程は、 だいたいはすぐ終わるが、 たまにすごく時間がかかることもある(指数分布)。 その結果、実験によって記録される反応時間のデータは、 両分布の足し合わせとしてのex-Gaussian分布になる、 と考えられたのである。 もちろん、少し考えてみれば分かるとおり、 脳内での意思決定過程にかかる時間が、 課題の種類に関係なくつねに指数分布するということはありそうもなく、 この理論は現在では否定されている。 しかしながらex-Gaussian分布は、 経験的には実際の反応時間データを非常によくフィッティングすることができるため、 現在でも反応時間解析において用いられている。 すなわち、ex-Gaussian分布における 「正規分布と指数分布の成分を判断過程と運動過程に帰する」 という仮説はもはや認められないが、 単純にフィッティングのための道具としてなら ex-Gaussian分布は使う価値があるといえるだろう。
反応時間解析に用いることのできる2つめの分布は、 shifted Lognormal分布だ。 Lognormal分布とは、正規分布の指数関数をとったときにできる分布である。 「ん?正規分布と指数って、ex-Gaussian分布でも出てこなかった?」 と思ってしまうが、 ex-Gaussian分布とLognormal分布はまったくの別ものである。 ex-Gaussian分布では、正規分布に指数分̇布̇を足し合わせることで、 右に長く尾を引く分布形状をつくりだしていた。 一方Lognormal分布は、正規分布を指数関̇数̇にいれたものである。 数学的にいえば、確率変数が正規分布にしたがうとき、 がしたがう分布がLognormal分布である。 こうしてできた分布を、横軸方向にいくらかシフト、すなわち平行移動させれば、 shifted Lognormal分布となる。 「シフト」というのは以降の分布でも何回かでてくるが、これは単純に、 反応時間は定義として正の値しかとらないので、 分布が正の値の範囲におさまるように平行移動しているにすぎない。 shifted Lognormal分布は、指数関数にかけるまえの正規分布がもっていたパラメータ・と、 平行移動の大きさという3つのパラメータをもつ。 詳細は省略するが、Lognormal分布は定義上、 複数のプロセスが直列につながれ、 それぞれのプロセスの結果の積のかたちで最終的な値が決まるようなシステムにおいて、 出力値の近似に有効である。 ただし反応時間解析においては、 そのような数学的特徴が重視されることはあまりない。 どちらかといえばshifted Lognormal分布も、 ex-Gaussian分布と同様に正の歪みをもつため、 反応時間データをフィッティングしやすいという経験的な理由により利用されているものと思われる。
3つめの分布はshifted Wald分布である。 この分布は、 正規分布や指数分布といった一般的な分布を変形して歪曲をもたせていた前2者とは、 かなり趣向が異なる。 Wald分布は、平均の正規分布で移動するランダムウォークが、 基準点を超えるまでにかかる時間のとる分布である(Figure 8)。

startから開始したランダムウォークが、 単位時間ごとに平均の正規分布の値で上下しながら、 基準点aのラインにまで達するのにかかる時間。 黒線は1回のランダムウォーク試行を、 みやすいよう色を替えて表示したもの。
shifted Wald分布は、この2つのパラメータに、 さきほどと同様のシフト項を加えた計3パラメータをもつ。 近年、多くの知覚弁別課題の神経機構が拡散モデルで説明されるようになってきたが、 このランダムウォークは、 まさに離散系における拡散過程である。 よってそのようなランダムウォーク過程から生じたshifted Wald分布を反応時間解析に用いるのは、 なにか意義がありそうに思える。 しかしながら、拡散モデルをあてはめることのできる心理課題はごく一部だけであり、 この分布を用いて反応時間データをフィッティングしたところで、 推定されたパラメータを心的証拠の蓄積速度や選択基準点といった、 拡散モデルにおける変数と直接結びつけて解釈するのは難しい。 結局のところこの分布も、 反応時間分布のフィッティングという文脈においては、 単に「正に歪曲していて使えそうだ」 という以上の意味はないと考えるのが妥当である。 ちなみに余段だが、 拡散モデルと知覚弁別過程との関係については、 非常にわかりやすい総説論文が多数発表されている。 こうしたモデルでは、 単純な反応時間データの分布形状の定量に止まらず、 意思決定から反応にいたるまでの内的な過程をモデル化することで、 実験から得られたデータをもとに、 課題内要因と反応のための心的過程との関係を調べることができる。 本解説文の読者にはきっと興味のある内容だと思われるので、 文献等を参照されたい。
他に反応時間解析に使えそうな分布としては、 shifted Weibull分布があげられる。 Weibull分布は「正規分布に似ているが歪んでいる理論分布」 の例として初等統計学にも登場する、 比較的有名な分布である。 平均の指数分布にしたがう確率変数の乗をとると、この分布になる。 Weibull分布のパラメータを直感的に説明するのは難しいのだが、 は尺度パラメータと呼ばれ、おもに分布の広がり具合に影響するのに対し、 は形状パラメータと呼ばれ、分布の形状を大きく変化させる。 これを反応時間データに合うようだけ平行移動してやったのが、 shifted Weibull分布である。 実用場面では、この分布でのフィッティングは、 故障率が経時的に変化するような部品の劣化現象の定量などによく用いられる。
本項で紹介する最後の分布は、Gumbel分布である。 Gumbel分布は指数関数を2回連続でかけたような特徴的な確率密度関数によって定義され、 二重指数分布とも呼ばれる。 この分布はこれまで紹介してきた分布と異なり、 とという2つのパラメータしかもたない。 は分布の位置を決定し、は分布の広がりに影響する。 一方この分布では、歪度はパラメータに依存せず、1.14という固定値となる。 このようにGumbel分布は、 分布の尾の部分に関する独立なパラメータをもたないので、 歪曲の度合いを任意に変化させることができない。 これは実際の反応時間データをフィッティングするうえでは大いに問題である。 そもそもこの分布は、 数学的には極値分布と呼ばれる一群の確率密度分布のひとつである。 極値分布は、 サンプルのなかに存在する基準値を超える観測値の数を記述するための分布であり、 いまわれわれが対象としている反応時間というデータとは、 およそ異なる性質の標本を扱うためにつくられた分布だ。 よってGumbel分布は、たしかに正の歪みはもっているものの、 なんらかの特別な理由がなければ反応時間解析に利用することはほとんどないと思ってよい。
2.3 ex-Gaussian分布を用いた反応時間解析
このように、反応時間データをフィッティングするための理論分布は、 乱暴にいってしまえば、 正の歪みをもったものならある意味なんでも構わない。 前項でとりあげた5つの分布も、 ケースによって分布ごとにフィッティングの良し悪しはあるだろうが、 どの分布でもそれなりに反応時間データをフィッティングすることは可能である。 しかしながら本項以降では、 これらのうちex-Gaussian分布を使った場合の解析方法に絞って説明していこうと思う。 なぜとくにex-Gaussian分布を取りたてるのかはすぐあとに述べる。 しかしそのまえに、まずはex-Gaussian分布の基本性質をまとめておこう。
ex-Gaussian分布は、 それぞれ正規分布と指数分布に独立にしたがう2つの確率変数があったとき、 その和がしたがう分布である。 統計学の記法を使うと、
| (3) |
ということになる。 ここで「」は「分布にしたがう」ことを意味し、 は平均標準偏差の正規分布、 は平均の指数分布を示している。 つまり上式を日本語に翻訳すれば、 「変数xが平均標準偏差の正規分布にしたがい、 変数yが平均の指数分布にしたがうとき、 合成変数z=x+yは・・ の3つのパラメータをもつex-Gaussian分布にしたがう」となる。
Table 1にも示したが、ex-Gaussian分布の確率密度関数は
| (4) |
である。 左辺のカッコ内に記されたx以外の・・が、 分布の形状を決める3つのパラメータであり、 とは正の値のみをとる。 また分布の基本的な統計量である平均・分散・歪度は、 数学的にパラメータとの関係が決まっており、それぞれ
| (5) | ||||
となる。 統計学の初学者にとっては、 統計量とパラメータとの概念的な違いがわかりにくいかもしれない。 具体的な3つの値・・を決めると、 それによって具体的なex-Gaussian分布がひとつ決まる。 この分布にしたがうような観測対象(確率変数)があった場合、 充分にたくさんのサンプルを記録すると、 データから計算される平均値はに一致する。 こうした規則性がEq.2.3 によって示した統計量とパラメータとの関係の意味である。
さてそれでは、 どの分布を使っても本質的にはおなじといいながら、 なぜ本解説文ではex-Gaussian分布をとりあげるのだろうか。 理由の第一には、ex-Gaussian分布の単純さがあげられる。 先述のとおりex-Gaussian分布は、 確率密度関数(Eq.2.3)こそ複雑にみえるが、 そもそもは正規乱数と指数乱数の和がしたがう分布であり(Eq.2.3)、 意味的に非常に単純である。 解析に単純な方法を使用することは、 解析結果の信頼性を高め、 他人にその結果を説明する際にも理解されやすくなる。 よってフィッティングの良し悪しに違いがないのなら、 shifted Wald分布のような「生い立ち」が複雑な分布よりは、 ex-Gaussian分布のように単純な分布を使うのがよい。
またより重要な理由として、 パラメータと分布形状の対応関係の分かりやすさがある。 先にも述べたとおり、ex-Gaussian分布は・・の3つのパラメータをもち、 ・は正規分布から、 は指数分布からそのまま受け継いだものである(Eq.2.3)。 よっての大小は分布のピークの位置、 はピークまわりの裾野のひろがり具合、 は右側への尾の引き方の長さという分布の特徴とそれぞれ1対1で対応する (Table 1a 最右列)。 これは実際のデータ解析において非常に大きな利点である。 たとえばex-Gaussian分布でのフィッティングの結果、 ある課題条件での推定値だけが大きくなっていたなら、 反応時間としてはピークを中心とするばらつき具合が大きくなったことを示している。 あるいは別の条件でが減少しが増加したならば、 正規分布的な釣鐘状の部分の中心は左に移動したものの、 同時に尾が右に長く引くようになったことを意味する。 とくにこの後者の例のような、 反応時間分布のピークと歪曲の同時変化は、 一般的な平均・標準偏差の計算だけでは絶対に定量できないものであり、 フィッティングを用いて解析を行なうことの大きなメリットである。
ex-Gaussian分布以外の分布の場合、 こうしたパラメータと分布特徴との対応はそれほど単純ではない。 たとえばshifted Lognormal分布のパラメータとは、 それぞれの増加によって分布のピークが逆方向へ動きながら、 裾野のひろがりや歪曲も変化している(Table 1b 最右列)。 またshifted Wald分布のとは、 その増減によって分布の形状が正反対の変化をみせていることがわかる(Table 1c 最右列)。 よってこれらのパラメータが同時に変化した場合、 分布の形状がじつのところどのように変わったのかを数値のみから読み取るのは、 非常に困難である。 そもそもex-Gaussian分布以外の分布におけるパラメータは、 シフト項を除き、 そのほとんどがピーク位置と分布形状の両方に影響を与えている。 そのためそれらのパラメータの変化の解釈は、 どうしてもex-Gaussian分布の場合より直感的でなくなる。
このようにex-Gaussian分布は、正の歪曲をもつ理論分布のなかでも、 その単純さやパラメータの解釈のしやすさから、 反応時間解析においてとくによく利用される。 そしてそのような解析を行なうことで、 単にデータの平均値や標準偏差を計算するだけでは定量し得なかった分布の形状の情報を、 正確に表わすことができるのである。 それでは次節で、このような解析を実際にRで行なうにはどうしたらよいか、 順に説明していこう。





 @kanri_ninjin
@kanri_ninjin



 イクナイ! 581
イクナイ! 581