1 反応時間データの歪曲と古典的解析手法
本節では、反応時間データの一般的な説明からはじめ、 反応時間の解析が心理過程を調べるためにどのように役に立つのかを説明する。 そのうえで、反応時間解析において古典的に用いられてきたいくつかの手法を概説し、 それらの問題点を指摘する。
1.1 反応時間
反応時間とは、 主体にある行動が求められてから、 実際にその行動が起こるまでにかかった時間のことである。 英語ではreaction timeとresponse timeというふたつの呼び方がある。 どちらかというと、前者は刺激に対する比較的単純な反応を求める場面において、 後者はより認知的な要求が高い課題において使われることが多いように思われる。 しかし、明確な定義の違いや厳密な使い分けはないようである。 いずれにしても、省略型はRTとなる。
心理学実験において、反応時間は正答率と並ぶ基本的な行動指標であり、 これを検討することによって、 課題条件間で必要とされる認知処理の違いや、 主体がとっていたストラテジーを推測することができる。 本項では、知覚心理学における古典たる視覚探索を例に、 反応時間のデータが心的過程についてなにを教えてくれるのかみてみよう。
視覚探索 visual searchは、 複数の視覚刺激を含んだ画面を呈示され、 そのなかに定められたターゲット刺激があるかどうかを判断して報告する、 単純な課題である(Figure 1)。

(a) 特徴探索の探索画面例 (b) 結合探索の探索画面例 (c) 探索課題における典型的な反応時間推移。 実線は結合探索、 点線は特徴探索を表わす。 特徴探索では刺激数が増加してもターゲットをみつけるまでの反応時間がほとんど増加しない (ポップアウト効果)。
たとえばFigure 1のa・bは、 非常に単純化された視覚探索課題の探索画面例を示している。 どちらの条件においても、実験協力者は右に傾いた(右肩あがりの)赤い線分を探索し、 それが画面内に存在する場合にはキー押しで報告しなければならない。 画面内にターゲットがない試行では、キーを押さずにいれば正答となる。 このとき、Figure 1aのように、 刺激のもつ単一の特徴(この例では「色」) にだけ注目すればターゲットか否かを見分けられるような視覚探索を、 特徴探索 feature searchという。 一方、Figure 1bのように、 「色」と「傾き」のような複数の特徴を合わせないとターゲットか否かを判断できないような探索を、 結合探索 conjunction searchという。
このようなふたつの探索条件を用い、 画面内に一度に出る刺激の数を何段階かで変化させ、 ターゲットが実際に存在した試行での被験者のキー押しの反応時間を調べると、 一般にFigure 1cのような結果が得られる。 破線は比較的簡単な特徴探索の、 実線はより難易度が高いと思われる結合探索の試行を示している。 これをみると、結合探索のほうが一貫して反応時間が長くなっており、 複数の特徴に注目する状況のほうがたしかに探索が難しいことが分かる。 しかしこのデータが示していることは、それだけではない。 刺激数の増加に対する、実線と破線の変化の仕方に注目してほしい。 結合探索条件では、画面内の刺激数が3・6・12と増えると、 それにともないターゲットをみつけるまでの時間も増加している。 これは刺激数が多いほど探索が困難になるということであり、直感的に理解できるだろう。 しかし破線で表わされた特徴探索条件においては、グラフがほぼ水平になっており、 刺激数の増加にともなう探索時間の増加がみられない。 これはすなわち、単一の特徴のみに注目すればよいような探索状況においては、 刺激の数が増えてもそれほど困難なくターゲットをみつけだすことができるということである。 このような特徴探索における探索効率の特性を、 ポップアウト効果 pop-out effectと呼ぶ。 これは特徴探索において、一度にたくさんの刺激を呈示した場合でも、 探すべきターゲットが「浮き出るようにパッとみつかる」ことから付けられた名称である。
これらの結果は、ヒトの視覚処理における重要な事実を示唆している。 それは、視覚情報の処理にはふたつの異なる様式があるということだ。 ひとつめの様式は、視野内の刺激にひとつひとつ注目し、 その詳細な特徴を検討していくという系列的な処理のプロセスである。 このような処理は、 複数の視覚特徴を合わせて判別しなければならない結合探索において使用されていると考えられる。 これは結合探索において、探索にかかる時間が、 刺激数の増加に比例して単調に増加していることからも支持される。 (ひとつの視覚刺激を処理するのに単位時間tがかかるとき、刺激がn個あれば、 それらすべてを処理し終えるのに必要とされる時間はtnとなりnに単純比例する11 正確には、n個の刺激を無作為な順で系列的に処理していくとき、 各刺激がターゲットである可能性は等確率なため、 平均的には半分まで探したところでターゲットがみつかり、 それにかかる時間はtn/2になる。 いずれにしろ、系列的に刺激を処理すれば、 ターゲットの存在を報告するまでに要する時間は、刺激数nに比例する。。) 一方、視覚情報処理におけるふたつ目の機構は、 視野内のすべての刺激を一括で処理するようなプロセスである。 これは視野のなかに存在する刺激の数に依存せず、 すべての刺激を並列的に処理する過程と考えられる。 このような情報処理は、一度に処理できる刺激数が多いぶん、 比較的単純な視覚特徴しか扱うことができず、 そのため特徴探索においてのみポップアウト効果がみられるのだと考えることができる。
このように反応時間は、 単なる主体のモチベーションや試行ごとの行動のランダムなばらつきのみを反映する指標ではない。 反応時間に注目することで、 課題中に主体が内的に行なっている認知過程を推測することができるのである。
1.2 反応時間データの歪曲
このように反応時間は、 反応が求められてから実際に起こるまでの時間という非常に単純な指標でありながら、 それを詳細に検討することにより、 直接観察できない主体の心的過程を推測することができる。 反応時間を「心理学実験におけるもっとも基本的かつ重要なデータ」 と表現したわけが分かっていただけただろう。
しかし反応時間のデータには、非常に一般的にみられる困った問題が存在する。 それはデータの歪曲 skewである。 たとえば、あなたがある単一の課題を行なって、反応までにかかった時間のデータを得たとしよう。 そのデータをもとに反応時間のヒストグラムを描くと、 Figure 2のような、 正規分布よりも左側に向かって歪んだような分布となることが非常に多い。

反応時間データにみられる典型的な分布歪曲の例
このようなデータの分布を「正に歪んでいる」という。 小さいほうの値に偏ってるのに「正」とは、ちょっと不自然に聞こえるかもしれない。 これは正規分布のような対称な分布と比べ、 データが正の方向に尾を引いていることからくる名称である。 分布の歪曲の度合いは歪度 skewnessという指標によって定量される。 歪度はデータX、データの平均m、標準偏差sとしたとき
| (1) |
で定義される指標で、 分布がFigure 2のように左に向かって傾き、 右側に長く尾をひいたような形状のとき、正の値をとる。 逆に分布が右に向かって傾いていれば、歪度は負の値をとり、 そのような分布を負に歪んだ分布という。 「正の歪曲」「負の歪曲」という表現と、 計算される歪度の符号とが一致すると考えれば覚えやすい。
反応時間のデータは、一般に正の歪曲をもつことが多い。 これは反応にある程度のタイムプレッシャーがあるとき、 すなわちできるだけ早く反応するように求められた状況なら、 概してみられる非常に一般的な特徴である。 動物実験では言語的なタイムプレッシャーがかけられないが、 その場合でも、 充分に素早く反応しなければ報酬のエサが与えられないような課題では、 必然的にタイムプレッシャーが生じる。 またそうした明示的な課題手続きなしでも、 一般に動物はできるだけ早く報酬を得ようとするため、 そこに潜在的なタイムプレッシャーがかかり、 やはり反応時間の分布は正に歪む。
なぜこのような歪曲がみられるのかについては、じつはさまざまな可能性があり、 それほど簡単ではない。 ただ一般論としては、以下のように考えると納得がいくだろう。 なるべく早く反応しようとするとき、反応時間は短くなり、分布は左に寄る。 しかし「反応を求められてから実際に行なうまで」という定義上、 反応時間が負になることはなく、 また筋の収縮にかかる時間などの不可避な成分を考えると、 おのずと反応時間の短縮はある程度であたまうちになる。 一方で長くなるぶんには時間は無限に長くなることができ、たくさんの試行を行なえば、 そのうち少数の試行では、注意散漫やキー押しのミスなどにより、 やたらと長い反応時間が得られてしまうことがある。 その結果、左に寄ろうとしたデータはある一定のラインで押さえつけられ、 右には尾をひくかたちで、分布が歪むことになる。
ともかく、原因の推測はさておくにしても、 実際問題として反応時間のデータは一般的によく歪む。 そこで反応時間解析においては、このデータの歪みをどう扱うかがポイントとなる。 もし分布の歪曲が単なる実験上のノイズであるならば、 難しく考えずともどうにかして歪みを除いてしまえばよい。 これは多くの慣習的な反応時間解析の手法がとってきた態度である。 しかし課題も条件も異なるさまざまな実験場面において、 反応時間分布の正の歪曲が一貫してみられるという事実は、 この歪みがただのノイズではなく、 反応時間という指標がもつ固有の特徴である可能性を示している。 すなわちデータにみられる分布の歪みが、 データを通して理解しようとしている主体の心的過程そのものがもつ性質だという可能性である。 もしそうだとすれば、 分布の歪みをただのノイズとみなして排除してしまうことは、 観察対象である心的過程についてデータがもつ情報を捨ててしまっているのに他ならない。 裏を返せば、 正の歪みをもった反応時間データから正しく情報を得るためには、 それに適した特別な方法が必要になる。
次項からはまず、 これまで慣習的に行なわれてきたいくつかの反応時間解析の方法を紹介し、 それらの方法だとなにが問題なのかを理解しよう。 それを踏まえ次節で、 より適切に反応時間データを解析するための手法を学習する。
1.3 代表値のみの利用
反応時間の解析を行なううえでもっとも荒っぽく愚直な方法は、 とくに難しいことを考えず、 「普段どおり」の平均値を用いてデータを要約することだろう。 つまり「歪んでいようがなんだろうが、全試行で平均化しちゃえば、 余計なものは消えるだろ」という思想である。 そしてこのような荒っぽいやり方が、 現実に存在する研究のなかでもっとも多く採用されている、 反応時間解析の方法である。
しかしながら、このような平均値を用いた数値要約は、 反応時間のように歪んだ分布をとるデータには一般に不適切である。 なぜなら平均値は、全観測値を平等に利用するがゆえにハズレ値の影響を受けやすく、 正に歪んだデータでは、概してデータを過大評価する傾向があるからである。 Figure 2における3つの矢印は、 このデータにおける平均値 mean・ 中央値 median・ 最頻値 modeの値を示したものである。 平均値は右に長く引いた分布の尾に引っ張られ、 実際のピークの位置よりもかなり右に寄っていることが分かる。 これは、たとえば「ある課題条件で平均反応時間が大きくなった」という情報だけでは、 それが分布全体が右に移動したためなのか、 あるいは分布がより長く右に尾を引くようになったためなのか区別できないということを意味している (Figure 3a)。
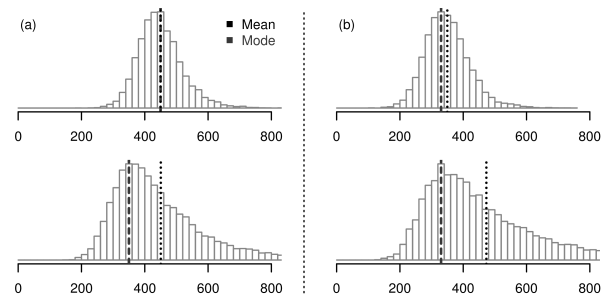
(a) 平均値は同じだが、ピークの位置が異なる分布の例 (b) ピークの位置は同じだが、平均値が異なる分布の例
ではFigure 2で分布のピークの位置を的確に示している、 最頻値を使うのはどうであろうか。 じつはこれもあまり得策とはいえない。 というのも、反応時間のデータは連続な実数なので、 まったく同じ観測値が複数回得られることは厳密にはあり得ず、 最頻値の算出にはデータの階級化 binning、 すなわちある一定の範囲(階級 bin) ごとにデータを区切って集計する作業が必要となる。 結果、得られた最頻値は階級化における範囲の設定に依存することになり、一意性に欠ける。 さらにそのようにして算出しても、 最頻値はたしかに分布のピークの位置を的確に表現はするが、 そのかわり歪曲した分布の尾の部分の情報はまったくもたず、 それだけではデータの特徴を表現しきれない。 これはたとえば、ふたつの課題条件間で最頻値が同じ場合でも、 一方の条件では他方より長く尾を引いた分布形状をしていることがあり、 最頻値だけではそういった差を見逃す危険性があるということだ(Figure 3b)。
このように、平均値をとればピークの位置が分からず、 一方で最頻値をとると分布の歪み具合の情報がなくなる。 これらの問題は、 結局のところ単一の代表値 central tendency を用いて反応時間のデータを要約しようとすることの限界を示している。 すなわち、 反応時間のデータは「ピークの位置」と「尾の引き方」 という少なくとも2つの分布特徴をもっており、 これを的確に定量するためには、 両者をふたつの異なる指標で評価してやる必要があるということだ。
1.4 ハズレ値の除外
しかし世の中には、 何でも平均化しないと気が済まないひとがどうにも多いらしい。 そういう人々が反応時間のような歪曲したデータを解析する際に使うさらに強引な解析方法として、 データにみられる極端な値をハズレ値 outlier として取り除くというやりかたがある。 その根底には、「分布が歪曲して極端な値があるせいで、 平均値がそれに引っぱられるのなら、 その邪魔者を消してやれば『正確な』平均が算出できるハズだ」 という思想が存在する。
たしかに、たとえば刺激が出たらボタンを押すだけの単純反応課題において、 1秒を超すような反応時間の試行があったら、 実験協力者がぼけっとしていたことによるハズレ値とみなして除外したいところだ。 しかし、そうまでしてピークの位置だけをみたいのであれば、前節でみたように、 平均値ではなく最頻値など、最初からハズレ値に強い指標を使えばよいのである。 そうすれば、 わざわざハズレ値として一部のデータを捨てるという前処理の必要はない。 また、そもそもどんなデータをハズレ値とみなすかに絶対的な基準は存在せず、 データ除外の操作は少なからず恣意的なものとなる。 よってそのような前処理を行なったデータはつねにサンプリングバイアスの危険を含み、 もとのデータがもっていた重要な特徴を見逃してしまうことさえあり得る。
先にも述べたとおり、 正の歪曲は反応時間分布に一貫してみられる普遍的な性質である。 よってそこには、反応時間というデータ形式が特有にもつ情報が含まれている可能性がある。 だとすれば、 反応時間データにおいてしばしばみられる極端に大きな値をハズレ値として捨て去ることは、 その情報を選択的に捨てているのと同義である。 このようなデータの性質を適切に定量するためには、 ハズレ値とみなしたくなるような 少数の極端な観測値が含まれることを最初から想定した解析方法が有用と考えられる。
1.5 変数変換
このように、反応時間がもつ分布の歪みという性質は、 データの特徴を要約するうえで絶対に無視できない。 そしてそれは、統計検定をするうえでも問題となる。
実験から得られたデータについて議論するとき、 数式に裏付けられた統計学的な検討は不可欠である。 統計学的検討なしに「この差は重要です」と主張しても、 誰にも聞いてもらえないだろう。 もちろん、世の中便利になったもので、 現在では自分で手計算をしなくても、 汎用のプログラムを用いれば簡単に統計検定を行なえるようになった。 しかしそのせいで、非常に多くのひとが、 確率論的な基礎の知識をおさえることなく、 無自覚に統計検定を濫用するようになってしまった。
どのような方法を用いるにしろ、ある手法を用いて検定を行なうとき、 そこにはそれを適用するうえで仮定される前提条件が存在する。 現在ひろく用いられているt検定や分散分析などの方法はパラメトリック検定と呼ばれ、 検定を適用するデータが正規分布にしたがっていることを前提とする。 パラメトリックな検定を正規分布にしたがわないデータに適用すると、 一般に検定力が低下し、本当は存在する差を見逃す可能性が大きくなる。 よってt検定や分散分析は、理論的に正規分布することが予想されるデータや、 経験的に正規分布に近い分布を示すようなデータにのみ用いられるべきである。
そのような観点からみれば、 Figure 2のように大きく正に歪んだ反応時間のデータには、 パラメトリックな検定はとうてい適用できそうにない。 もちろんそういった場合でも、ノンパラメトリックな方法を使うといった代替法は存在する。 しかし不思議なことに、 世の中には「統計検定といえばt検定か分散分析でないと許せない」 という変わった信念をもった方々がとても多い。 そういったひとたちが、 反応時間のような正規分布しないデータに無理やりパラメトリック検定を適用するために用いるのが、 変数変換 transformation of variableである。 変数変換とは、データに対して特定の変換を行なうことで、 分布の形状を変化させる手法である。 分布の形状を変えたいので、変換は一般に非線形となる。 (線形な変換はデータを拡大・縮小・平行移動させるだけで、分布の特徴は変化しない。) ここではパラメトリックな検定を適用できるようにしたいわけだから、 データの分布を正規分布に近づけることが目標になる。 反応時間解析においては、 経験的に対数変換 logarithmic transformationを用いることが多く、 これにより多くの反応時間データが正規分布に近づくことが知られている(Figure 4)。
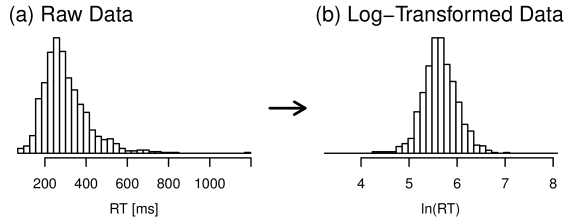
正に歪んだ反応時間分布(左) とそれを自然対数により変換した後の分布(右)
このような変換をほどこし、データの分布を正規分布に近づけてから、 パラメトリックな統計検定を利用して条件間での差などを検討するわけである。 対数の底は(1より大きければ)それほど変換の結果に影響しないが、 慣習的には自然対数で変換することが多いようだ。
たしかに、このような方法を用いれば、 正に歪んだ反応時間の分布を正規分布に近づけることができ、 お決まりのt検定や分散分析を解析に用いることができるようになる。 しかしここで注意しなければならないのは、 そのような検定の結果みられた有意差はあくまで変数変換後の値に関して保証されるものであって、 変換をほどこす前の(ナマの) 反応時間においても差があるといえるかどうかは分からないということである。 すなわち条件Aと条件Bでの反応時間・ に関して変数変換適用後に検定を行なった場合、 主張できるのはとの大小関係の確からしさであり、 と のあいだに有意とみなせる差があるかどうかはまたべつの問題なのだ。
また、そもそも変数変換は、 変換後の確率変数が正規分布にしたがうことを理論的に保証するものではない。 単に「こういう風に変換すると、なんとなく正規分布っぽくなるよ」という変換方法を、 経験的に利用しているだけである。 よって変数変換を行なっても、結局は分布が正規分布にはならず、 パラメトリックな統計手法を適用できないこともある。 変数変換によって正規分布になることが保証されるのは、 もともとの確率変数が正規分布に変換の逆関数をかけた分布にしたがっていた場合のみである。 対数変換の例でいえば、 もとのデータが対数正規分布にしたがっているという理論的根拠がある場合のみ、 変換によりデータが正規分布にしたがうようになることが保証される。 しかしながらもしそのような生のデータの母分布に関する知識があるのであれば、 なにも変数変換後にパラメトリック検定などをする必要はない。 最初からその母分布を仮定した、母分布に合った解析手法を使ってやればよいはずだ。
このように変数変換は、 母分布に関する事前知識がなければ変換後の分布が正規分布になる根拠がなく、 一方で母分布の型が分かっているのであればそもそも使う必要がない。 またわざわざ変換してまで行なった検定は、 変換後の値に関しての情報しかもたず、 変換前のもとのデータに関して有意な差があるかどうかは分からない。 変数変換は、現在のようにさまざまな統計手法が整う前、 まだ基本的なパラメトリック検定ぐらいしか研究者に武器がなかったころに、 なんとかして手持ちの道具で戦うために編み出された方法である。 よって現在では、よほどの理由がなければ、 わざわざこのような方法を使う意味はない。 この平成の時代においても、 いまだに「反応時間の検定なんだから対数変換かけろ」 「正答率の検定なんだから逆正弦変換かけなきゃおかしい」 といった残念な固定観念に縛られている研究者がいるが、 そういった輩は心のなかで一笑に付しておけばよいだろう。 (態度に出すと深刻な人間関係の問題を生む場合があるため、 表面上は適当に取り繕っておくこと。)





 @kanri_ninjin
@kanri_ninjin



 イクナイ! 581
イクナイ! 581