1 神経細胞と静止膜電位
ヒトの脳は約1000億個という膨大な数の神経細胞からなり、 それらの細胞の活動こそが、 ヒトの運動・感覚・思考・記憶・感情といったさまざまな肉体的・精神的機能の根本である。 神経細胞を知ることは、 ヒトについて知ることの第一歩であり、 また同時にそのための究極の方法であるともいえる。 本節では、神経細胞の構造とその性質について概説する。
1.1 神経細胞
神経細胞 nerve cell(ニューロン neuron) は形態的にも機能的にも非常に特殊化した細胞である。 Figure 2に一般的な神経細胞の模式図を示す。 高等学校で生物学を履修したひとには、 お馴染みの図かもしれない。 しかし実際のニューロンがみな、 本当にこの模式図のような格好をしていると考えるのは間違いだ。 ひとくちにニューロンといっても、 その形態は機能に応じて多種多様である。損傷例研究や機能的脳イメージングなど、 巨視的なレベルの神経活動を研究対象としているとつい失念しがちだが、 神経科学の知見の複雑さに触れるとき、 その根幹には神経系の構成単位たるニューロンの複雑が座しているという事実を忘れてはならない。
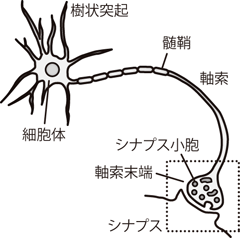
ニューロンがこのように特異な形状をしているのは、 この細胞が複雑なネットワークを形成し、 情報の入出力を行なうためである。 ニューロンの細胞核が存在し、 比較的広い部屋のようになっている部分を 細胞体 soma(cell body)という。 細胞体から周囲に突き出した木の枝のような構造は 樹状突起 dendriteと呼ばれ、 他の細胞から情報入力を受けるための場所である。 脳の部位やニューロンのタイプによって幅はあるが、 1つのニューロンは他のニューロンたちから、 1万を超える膨大な数の情報入力を受ける。 一方、細胞体からは軸索 axon と呼ばれる長い突起が1本(ニューロンの種類によっては2本)伸びており、 これは他の細胞へ情報を出力するための構造である。 軸索はその途中や末端部においてたくさんの分枝を出し、 平均1000個以上のニューロンに対して連絡する。 このニューロンとニューロンの接点のことをシナプス synapseという。 シナプスにおいて、ニューロンは次のニューロンへと一方向性に情報を伝達する。
以上のようにひとつのニューロンは多数の入力を受け、 多数の対象に対して出力を行なう。 一般的にいってこのような素子により構成されるネットワークは複雑を極める。 1000人以上のひとの意見を参考に、 あなたが何かを心に決め、 それをまた1000人以上の他人へと伝える。 そんなひとが1000億人集まってできているのが脳なのだ。 この気の遠くなるほど複雑なネットワークこそ、 われわれの脳・神経系のもつ本質的特徴である。
1.2 ニューロンの運ぶ情報
先ほどから「情報」ということばを使っているが、 ニューロンが運ぶ情報とはいったいどんなものなのか。 たとえば暑い部屋の中にいるときのことを考えてほしい。 周囲の温度を感知するのは皮膚の温度受容器細胞である。 しかし「気温が高い」という外界の現象に対して、 それを「暑い」と知覚し、 何らかの行動をおこさせるのは脳である。 この皮膚と脳との間を神経細胞がつないでいる。 このとき、いまとるべき行動を脳が適切に判断するためには、 部屋が「どれだけ」暑いのかという情報が不可欠である。 蒸し風呂のような暑さの部屋からは一刻も早く逃げ出す必要があるが、 少し汗ばむ程度なら、 わざわざ行動を起こすほどのこともない。 よって、皮膚から伝えられた情報をもとに脳が身体を制御するなら、 ニューロンが運んでいる温度情報は、 多寡の区別が可能な数値情報として表現されていて然るべきである。
しかし実際のところニューロンは、 「伝えるか伝えないか」すなわち「1か0か」というon/off制御によって情報を伝えている。 これはコンピュータによる1/0のデジタルな情報処理・保持機構とよく似ている。 コンピュータのメモリやハードディスクにおけるデジタル信号は、 コンデンサなどの素子の蓄電/非蓄電という2つの状態によって保持されている。 一方ニューロンにおいてこのデジタル情報を表現する物理的実態は、 細胞内外の電位差の状態である。 ニューロンは一過性に細胞内外の電位差を変化させる機構をもっており、 それによって活動電位 action potential と呼ばれるパルス的な電気応答をする。 この「活動電位を発している(1)」か「発していない(0)」かということが、 ニューロンにおけるデジタルな情報表現の実装なのだ。
このように単一のニューロンが伝えるうる情報は1か0かの2値だけである。 では先ほどの温度の例のような「刺激の量」の情報は、 いったいどうやって伝えられているのだろう。 これは単一ニューロンにおいては単位時間内における活動の頻度によって、 またニューロン集団においては集団全体に対する活動しているニューロンの割合によって伝えられている。 こうした情報表現の詳細は、 それぞれの感覚・運動システムによって異なっているため各論に譲ることにする。 ひとまず本節では、 ひとつのニューロンがその情報単位である活動電位を発生する仕組みの学習に専念しよう。 次項では、まず活動電位が発生するための前提である、 ニューロンの電気的性質について説明する。
1.3 静止膜電位
前項で述べたように、 ニューロンの伝える情報は活動電位という電気信号の形で細胞内に表現される。 活動電位とは細胞の電気状態の一過的変化であり、 ある瞬間、 活動電位が「ある(発している)」か「ない(発していない)」かのon/offの違いこそが、 ニューロンの情報表現の単位なのだった。 この活動電位について知るためには、 まず活動電位を発していない通常状態のニューロンがもつ電気的性質を知らなければならない。
ニューロンが活動電位を発していない状態のことを 静止状態 resting stateといい、 このときニューロンは静止膜電位 resting potential と呼ばれる電気的状態にある。 静止膜電位とは、読んで字の如く「静止状態のときのニューロンがもっている電位」 のことである。 より正確に言えば「活動電位を発生していない状態のニューロンの細胞内部が、 細胞外部に対してもっている電位」のことを静止膜電位と呼ぶ。 すなわちニューロンは、 活動状態にない場合でも細胞内外で電位差を生じており、 そのとき細胞外を0mVとみなした場合の細胞内の相対的な電位が静止膜電位である。 一般的な神経細胞では細胞内は細胞外に比べて負に帯電しており、 静止膜電位は-75〜-60mV程度というマイナスの値を示す。 イメージのために例をあげると、 これは静止状態のニューロンの細胞内外を導線でつなぐと、 細胞外から細胞内へと電流が流れるということである。 すなわち神経細胞は(じつは他の一般的な細胞もまったく同じなのだが) まるで電池のように蓄電した状態にあるのだ。
しかしエントロピー増大則(熱力学の第二法則)が示すとおり、 自然界の事象はかならず乱雑な(エネルギー的に均一な)状態に向かうよう、 運命づけられている。 細胞の内側が外側よりマイナスに保たれるなどというエネルギー的に不安定な状態は、 特殊な機構なしでは決して生じ得ない。 では静止膜電位はいったいどのようにして生じているのだろうか。
Table 1は一般的な体内環境において、 ニューロンの細胞内外に存在する主要なイオンの濃度である。 この表から明らかなように、 神経細胞の内外には非常に大きなイオン濃度の差がある。 これが静止膜電位の維持に貢献する一人目の役者であり、 細胞膜をはさんだイオン濃度勾配 ion concentration gradientとよぶ。
| イオン種 | 細胞内濃度 | 細胞外濃度 |
| K+ | 150 [mM] | 5.5 [mM] |
| Na+ | 15 [mM] | 150 [mM] |
| Cl- | 9 [mM] | 125 [mM] |
| (ネコ運動ニューロン) | ||
このような細胞内外でのイオン濃度の差は、 細胞膜がイオンを透過しないからこそ保たれている。 細胞膜は脂質二重層という疎水的(電気的に中性)な構造でできているため、 電荷をもったイオンのような粒子は通り抜けられないのだ。 しかし一方で細胞膜上には、 細胞内外の物質を能動的/受動的に輸送するさまざまなタンパク質が存在している。 このようなタンパク質のうち、 K+リークチャネル potassium leak channel (K+漏洩チャネル) と呼ばれる分子が、 静止膜電位の発生に関わるもうひとりの役者である。 K+リークチャネルは膜をはさんだふたつの溶液におけるK+濃度にしたがい、 K+だけを選択的にかつ受動的に透過する。 すなわちK+リークチャネルは濃度の高いほうから低いほうへとK+を通す、 文字通り「チャネル(水路)」である。 このK+リークチャネルの存在により、 通常ではイオンを通さない脂質二重層の細胞膜を、 K+だけがすり抜けて細胞内外を拡散できる。 このように細胞膜が種々の膜タンパクによって特定のイオン種のみを透過する性質を、 膜の選択的透過性 selective permeabilityという。
これで役者はそろった。 このような「細胞内外のイオン濃度差」と「細胞膜の選択的イオン透過性」が存在するとき、 ニューロンの静止膜電位は自然な帰結として生じる。 これを理解するために以下のモデルを考えてみよう。
いまFigure 3の細胞モデルにおいて、 細胞内に酢酸カリウムが存在し、 カリウムイオンをK+、酢酸イオンをA-と表わすこととする。 カリウムイオン(K+)はリークチャネルを介して膜を透過することができるが、 酢酸イオン(A-)のような大きな分子は膜を通り抜けることはできない。
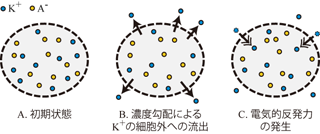
このときK+だけに注目してみよう。 K+の濃度は細胞外(K+0個)より細胞内(K+10個)の方が高い。 そこでK+はこの濃度勾配にしたがい、 リークチャネルを通って細胞外へと流出する。 もしK+に電荷がなければ、 この流出は細胞内外のK+濃度差がなくなるまで続くだろう。
しかしK+粒子は+1という正電荷をもつため、 K+が細胞内から細胞外へ1個流出するごとに細胞外は少しだけ正に帯電し、 逆に細胞内は負に帯電する。 もしA-が膜を透過できればK+と同じだけA-も流出すればすむはなしだが、 残念ながらA-(ここでは酢酸イオン)は膜透過性をもたない。 こうして細胞内は外に対してマイナスに帯電し、 このとき生じる電場によって、 プラスのK+には細胞外から細胞内へ引き戻そうとする力がはたらく。 つまりK+が濃度勾配に従って細胞外へ流出すると、 K+の拡散に電気的なブレーキがかかっていくのである。
最初濃度勾配によるK+流出は電場による(細胞内への)吸引力にまさっており、 K+はどんどん細胞外へ拡散していく。 しかしK+の流出ごとに電場の力が強くなり、 その電場によって細胞外から細胞内へと引き戻されるK+の流入量が増加する。 そしてやがてK+の流入と流出がつりあったところで、 濃度と電位の変化が見かけ上とまる。 実際には濃度勾配によるK+流出も電場によるK+流入も起こり続けているが、 収入と支出が釣り合っているので、 細胞内外のK+濃度は総体として変化しない。 このとき細胞内は濃度勾配による拡散を引き止めるために、 細胞外に対して負の電位をもつことになる。 この電位をK+の平衡電位 equilibrium potentialという。 すなわち細胞内外にTable 1のようなK+の濃度勾配があり、 かつ細胞膜がK+を透過させる場合、 細胞はこのK+の平衡電位と同じだけの電荷を保持することで、 濃度勾配によるK+の流出を補償する (見かけ上K+の流入出を0にする)ことができるのである。 ここで平衡電位とは、ある一種のイオンに関して、 細胞内外で濃度差が存在し、 かつそれが少なからず膜を透過することができるなら、 そのイオン種に対してひとつ決まる値である。 すなわち平衡電位というのは、 膜を通り抜けることができるすべての生体内イオンについて、 それぞれひとつずつ定義される値であることに注意してほしい。
1.4 ネルンスト式
前項では静止状態のニューロンが静止膜電位と呼ばれる(細胞外に対する) 負の電位を有していることを説明し、 そのような負の帯電状態がK+の細胞内外濃度差と膜透過性によって説明できることを示した。 ここで思い出してほしい。 ニューロンの静止膜電位は、 細胞外に対しておよそ-75〜-60mVという値をとるのだった。 もしこれがK+の漏洩に起因するのであれば、 この値はK+の平衡電位と一致するはずだ。 それを検証するためには、 Table 1に示したような細胞内外のK+濃度において、 K+の平衡電位がどの程度になるかを計算する必要がある。 これを可能にしてくれるのが、 ネルンスト式 Nernst equationと呼ばれる計算式だ。
| Eion : | 平衡電位 |
|---|---|
| R : | 気体定数 8.31 [J/mol・K] |
| T : | 絶対温度 [ケルビン] |
| F : | ファラデー定数 96500 [C/mol] |
| z : | イオンの価数 |
| ln : | 自然対数 |
| [ion]out : | イオンの細胞外濃度 |
| [ion]in : | イオンの細胞外濃度 |
眠気を抑えて式を眺めてもらえば分かるとおり、 この式の右辺において、 変数は[ion]outと[ion]inだけである。 イオン種はK+なのだからzは+1に決まるし、 温度は一定とすればよい。 (こういう場合、とりあえず常識的な温度として、 常温25℃ = 298Kを使っておく慣習になっている。) そしてこの式によって求められる左辺の値が、 そのような膜内外イオン濃度とちょうど釣り合う膜電位の大きさである。 すなわち ネルンスト式は細胞内外のイオン濃度から平衡電位を求めることができる式なのである。 そこではこれとTable 1に挙げた数値を用いて、 K+の平衡電位を求めてみよう。
実際にイオン濃度を入れるまえに、 イオン種に依らない定数値を式に代入し、使いやすい形に変形しておくと、
となる。 ここへTable 1のK+に関する値、 すなわち [ion]in = 5.5, [ion]out = 150, z = 1を代入すると
となる。 これがK+の平衡電位である。
1.5 平衡電位と静止膜電位
「おやおや?静止膜電位は-75〜-60mVだと言ったくせに、 K+の平衡電位はもっと低いじゃないか。」 そのとおりだ。 これはニューロンの細胞膜は厳密にK+ だけを透過しているわけではないということを示している。
もし細胞膜が完璧にK+だけを透過しているのならば、 K+の濃度勾配と釣り合うだけの平衡電位-84.7mVが、 静止膜電位そのものとなるだろう。 しかし細胞内外にはK+以外にもNa+やCl- などのイオンが存在する。 これらのイオン種は膜によって妨げられながらも多少は細胞内外を移動し、 膜電位に影響を与えている。
たとえばNa+についてK+と同様に平衡電位を計算してみると、
となり、 Na+は細胞外に対して細胞内をプラスに帯電させる方向にはたらく ことが分かる。 これはNa+がK+とは逆に細胞外に多く、 濃度勾配によってNa+が流入すると、 細胞内に正の電荷が運ばれることになるためだ。 よってNa+が(K+と比べると少ないが)膜を透過することで、 膜電位がK+の平衡電位より少し上がるということが分かる。 このような他のイオンの効果のために静止膜電位はK+の平衡電位と正確には一致しない。 (K+以外のイオンがどうやって膜を透過しているのかは、 じつのところあまりよく分かっていない。 ただ、イオンのような荷電粒子に対する脂質二重層の透過性は非常に低く、 実験的に知られている細胞膜のNa+やCl-透過性よりはるかに小さい。 よってNa+やCl-は、 「無地」の細胞膜表面を通り抜けているのではなく、 膜上に少数存在する未知のリークチャネルや、 不活性状態の電位/リガンド依存性チャネルなどを無理やり通ることで、 静止膜電位に影響を与えているものと考えられている。)
「ちょっと待て。 静止膜電位(-75〜-60mV)がK+の平衡電位(-84.7mV)よりも弱いってことは、 濃度勾配に基づく拡散を引き止めるだけの電場が生じてないってことだろ? だとしたらK+は、 静止膜電位において、 濃度勾配にしたがって細胞外へ流出し続けちゃうじゃん。」 そのとおりである(再)。 静止膜電位においてK+は細胞外へと流出し続けている。 そのまま放置しておけば、 K+は内外の濃度差が静止膜電位で引き止められる程度に小さくなるまで流出を続けてしまう。 たとえば静止膜電位を-70mVで固定とし、 [K+]outを5.5mMとするなら、 [K+]inはネルンスト式から84mMでなければならない。 すなわち[K+]inが150mMから84mMになるまで、 細胞内から細胞外へとK+流出が起こってしまうわけである。 (ちなみにこの計算上では、 細胞内から多少K+が漏れ出したとしても、 [K+]out がほとんど変化しない程度に細胞外環境は広大だと仮定していることになる。)
そこで実際のニューロンにおいては、 Na+-K+ポンプ sodium-potassium pump と呼ばれる膜タンパクが、 流出した分のK+をATPエネルギーを消費して細胞内へと汲み戻している。 こうしてK+は平衡電位と少しズレた静止膜電位においても、 内外の濃度差を一定に保っていられるのである。 この関係をFigure 4に示した。

ちなみにNa+-K+ポンプは、 細胞外に流出していくK+を汲み取るのと交換で、 細胞内に少しずつ染み込んでくるNa+を吐き出している。 つまりNa+-K+ポンプは、 交換輸送によってK+とNa+の細胞内外濃度を保っているのだ。
ところで、 静止膜電位の値は正確にはK+の平衡電位と一致しないのに、 なぜか「静止膜電位はK+リークチャネルのはたらきで生じる」と表現される。 じつはこれは、もう少し正確にいうなら 「静止膜電位の-75〜-60mVという値は、 おもにK+の平衡電位の寄与によって決まっている」という意味である。 すなわちニューロンの静止状態においては、 種々のイオンが静止膜電位に影響を与えているが、 もっとも影響力が大きいのがK+の平衡によって生じる電位なのである。 これはK+がリークチャネルを通って細胞内外を自由に拡散できるのに対し、 他のイオンはそれと比べて膜透過性が低く、 少ししか細胞内外を移動できないことに因っている。 参考までに、 Table 1の細胞内外イオン濃度をもとに各イオン種の平衡電位を計算すると、 Table 2のようになる。
| イオン種 | 細胞外/内濃度 | 平衡電位 |
|---|---|---|
| K+ | 5.5/150 [mM] | -85 [mV] |
| Na+ | 150/15 [mM] | +59 [mV] |
| Cl- | 125/9 [mM] | -67 [mV] |
ときにこの表、 少々コンパクト過ぎではある。 分子細胞生物学に詳しい人は、 K+・Na+・Cl-の3種類だけをして 「細胞環境に存在する各イオン」と表現することを気持ち悪く思うだろう。 生体の細胞内外にはこれらに限らず、 Ca2+やMg2+、 HCO3- など種々のイオンが存在しているからだ。 それなのになぜK+・Na+・Cl-だけを取り沙汰すのか。 それは静止状態のニューロン環境に存在するイオンのうち、 ある程度の濃度があり、 かつ膜浸透やチャネルによって細胞膜を多少なりとも透過できるのが、 おもにこれらの3種だからだ。 先にみたように、膜に電位が発生するためには、 濃度勾配にしたがってイオンが膜の内外を移動しなければならなかった。 そのため、 静止状態のニューロンの細胞膜をあまり透過できないCa2+ などは表から除かれているのである。
さて先述のとおりK+とNa+は、ニューロンの細胞膜上の Na+-K+ポンプと呼ばれるタンパク質により、 濃度勾配に逆らうようにして交換輸送されているのだった。 すなわちK+やNa+は、 各々の平衡電位と実際の静止膜電位が異なるぶん、 膜を超えて少しずつ拡散しているため、 そのままでは細胞内の[K+]はどんどん減少し、 一方で[Na+]は細胞外からの流入によって増加してしまう。 これをATPエネルギーを用いて同時に補償する、 すなわち漏れ出た分のK+を引き戻し、 入ってきた分のNa+を排出するのがNa+-K+ポンプであった。 こうしてK+やNa+は細胞内外の濃度差を保たれているわけだ。
このようにこれらのイオンの濃度が一定に保たれるという前提条件 のもとでネルンスト式から平衡電位を計算すると、 Table 2のようにK+は-87mV、 Na+は+59mVである。 そして実際のニューロンで観察される静止膜電位が K+の平衡電位に近いということこそ、 K+の平衡が静止膜電位に与える寄与が非常に大きいということを示している。
と、ここで注意深い方ならお気づきと思うが、 なんとCl-の平衡電位は静止膜電位の-75〜-60mVという値におさまっている ではないか。 しかも実験的に、 Cl-はそれなりに細胞膜を透過するということが分かっている。 だとすれば、 じつはカリウムイオンでなく塩化物イオンのほうが静止膜電位を決定しているのではないか?
しかし答は「No」だ。 なぜならCl-にはNa+-K+ポンプのように濃度を一定に保つ機構がないからである。 つまりCl-の濃度は細胞の電位によって左右され、 その電位とちょうどつりあうような濃度差を保った状態になってしまうのである。 言い換えると、 細胞内のCl-の濃度は細胞の電位差によって受動的に決定される。 ということは、先ほどCl-について 「平衡電位が静止膜電位と一致しているから、 これが静止膜電位を決定しているのではないか」 と考えたのは、じつは因果が逆だったのだ。 実際は「静止膜電位によってCl-の濃度が決定されている」わけである。 なんとも紛らわしいハナシだ。
Na+やCl-が静止膜電位にそれほど影響していないということは、 細胞外にこれらのイオンを多量に加えても、 膜電位がたいして変化しないということからも示唆される。 逆にK+を細胞外に加えていくと、 それにつれて膜電位が上がっていくことから、 K+が静止膜電位の決定に大きく関わっていることも分かる(Figure 5)。
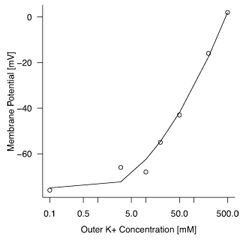
イカ巨大軸索において、 細胞外K+濃度をさまざまな値に変化させたときの、 軸索内外での電位差。
1.6 分極・脱分極・過分極
もし濃度勾配も透過性もなしに、 膜によって内部と外部を区切ったとしても、 内外の組成がまったく同じなのだからそこに電位差は生まれず、 内側は外側に対して0mVである。 しかし実際の生体細胞の場合、 内部のイオン組成は外部と著しく異なっており、 また膜上にはある種のイオンだけを通すイオンチャネルが存在するため、 細胞内外には電位差が生じたのだった。
このとき細胞内が外部に対して電位差を持っていることを 分極 polarizationしているという。 分極の「極」は「電極」の意味だと思ってもらえれば分かりやすい。 「極が分かれる」すなわちプラス側とマイナス側が生じるということである。 また細胞の電位が0mVに近づくことを脱分極 depolarization、 逆に0mVから離れることを過分極 hyperpolarizationという。 分極状態から「脱」するか、あるいは「過」度に分極するかということだ。
さて一般的な神経細胞は、 K+の濃度勾配とリークチャネルによってマイナスに分極していた。 よってこの状態において、 脱分極とは細胞内の電位が静止膜電位よりプラスに変動することにあたり、 逆に過分極はマイナスに変動することと対応する(Figure 6)。
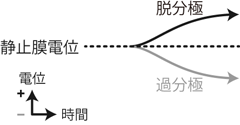
このように、 もともとの脱分極・過分極の定義には正負の意味合いはないのだが、 神経科学においては、 静止膜電位との関係においてそれぞれプラス・マイナスの意味をもって使われる。 これらの用語は以降の説明でも頻繁に登場するので、 ここで使いこなせるようになっておいてもらいたい。
コラム1: 透過係数とゴールドマンの式
Na+が静止膜電位の決定に関わらない理由として、 このイオンがほとんど膜を透過しないということを挙げた。 このように、 あるイオンが膜電位にどれだけ大きな影響を与えるかは、 そのイオンがどれほど膜を通りやすいかによって決まる。 イオンの膜透過性の高さは、 透過係数という指標によって表わされる。 透過係数はP元素名の形で表わし、 カリウムならPK、 ナトリウムならPNaとなる。
ネルンスト式はこうした透過性の大小は考慮せず、 そのイオン種が自由に膜を透過できる条件下において、 膜内外の濃度勾配による拡散と釣り合うだけの電位差(平衡電位)をもとめる式だった。 一方でこの透過係数を用い、 イオンごとの透過性を考慮しつつ膜電位を求めるための ゴールドマンの式 Goldman equation (ゴールドマン-ホジキン-カッツの式 Goldman-Hodgkin-Katz Equation)という計算式が存在する。 膜を透過するイオンをK+・Na+・Cl-の3種とした場合、 ゴールドマンの式は
となる。 iとoはそれぞれinとoutを差す。 Cl-において分母・分子が他のイオンと逆なのは、 陰イオンであるためだ。
では試しにこの式を使ってみよう。 実験的に求められた膜の性質として、 これらのイオンの透過係数比はおよそ PK:PNa:PCl = 1:0.04:0.45である。 よって
とおいてやると、分母・分子からPKを約分できて
となる。 この式から、 たとえばNa+が膜電位に果たす役割はK+と比べると25分の1になり、 [Na+]が多少変化したところで静止膜電位に大きな影響がないことが定量的にも理解される。 上式にTable 1のイオン濃度を代入してやれば、
となり、 K+単体でもとめた平衡電位と比べて、 静止膜電位の実測値により近い値が得られる。





 @kanri_ninjin
@kanri_ninjin



 イクナイ! 581
イクナイ! 581