たべっ子どうぶつの研究

たべっ子どうぶつの集計および解析結果を紹介します。
サンプルが増え次第、順次データは足していきます。

各回の調査結果概要

第1回 箱内調査

調査実施日：2013年10月21日

第2回 箱内調査

調査実施日：2013年10月26日

第3回 箱内調査

調査実施日：2013年10月30日

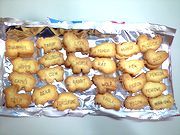
第4回 箱内調査

調査実施日：2013年11月05日

第5回 箱内調査

調査実施日：2013年11月16日

第6回 箱内調査

調査実施日：2013年11月22日

第7回 箱内調査

調査実施日：2013年11月25日

第8回 箱内調査

調査実施日：2013年11月29日

第9回 箱内調査

調査実施日：2013年12月06日a

第10回 箱内調査

調査実施日：2013年12月06日b

第11回 箱内調査

調査実施日：2013年12月12日

第12回 箱内調査

調査実施日：2014年01月07日

全体傾向およびどうぶつ種の割合

ひと箱に含まれるピース数

ひと箱に含まれていたピースは、平均45.5個。
最少で44個、最多で47個であった。
ゆらぎはあるものの、内容量はわりと安定しているだろうか。

また上記の写真記録時には、割れたピース片の除去などはしていないが。
にもかかわらず、分類からあぶれた余剰ピースはほとんどない。
すなわち、開封時点ですでに割れているピースは多数あるが。
そのほぼすべてが、断片を集めることで1個体に復元できた。

よって本製品において、ピースの断片化は封入前の時点ではほとんどなく。
封入時ないし封入後の移送等により、破損が起きていることが示唆される。

全調査結果における内訳

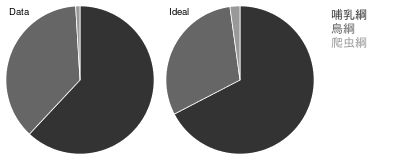
すべての集計結果の積み重ねグラフ。
各サンプルを異なる濃さのグレーで表示。
たしかにデータ上は、
という議論をしたくなる位には、種間差がみられる。

ちなみに横軸のラベルの色は、以下にも示す分類の別による色分け。
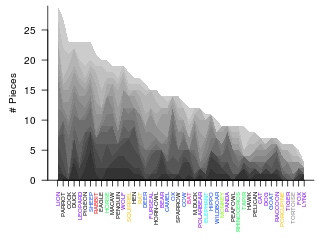
鳥綱は黒、爬虫綱は灰色。
哺乳綱はさらに目のレベルで別カラー表記。

分類階層での集計

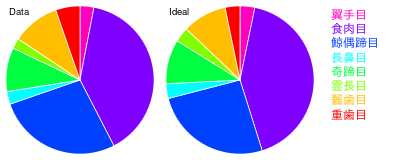
異なる分類階層レベルで内訳を詳細に検討。
左が実データ、右が全種が等確率と仮定した場合の理論分布。

まず種のレベルでの内訳。
これは要するに、上記の積み重ねグラフを別表示しただけ。
等確率なら、右図のように完全な等分の分割になるが。
実際には左図のように、多いのも少ないのもある。

次に綱のレベルでの内訳。
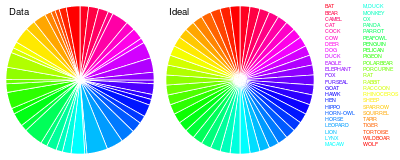
もとのラインナップ的には哺乳類がいちばん多く、つぎに鳥類が多い。
爬虫類はTORTOISEの1種のみ。

実際の集計をみると、やはり理論分布とは若干の違いがあるが。
大局的な傾向としては、むしろ内訳はわりと一致しており。
個々の種でみたときより、データのゆらぎは目立たない。

いちばん多い哺乳綱を、さらに目のレベルで分類してみる。
やはりここでも、データにおける固有の傾向というのは目立たず。
概ね理論分布に一致した出現頻度のように見受けられる。

このように、たしかに集計結果にはばらつきがあるが。
どちらかといえば、むしろおもったほどの偏りはない印象で。
すくなくとも
という議論には、あまり意味があるようには思えない。

実際、本研究と類似の調査報告がいくつかネット上にみつかるが。
どの種が多いかは調査ごとにまちまち。
しかも製造元は、全種がおなじ割合であることを公開している。

すなわち、どの種が多いかの議論にはあまり意味がない。
よって本研究では、以降、
のような、単純な種間比較とは独立な分布特性について検討していく。

箱単位の内容

全種そろえるのに必要な箱数

今回の調査では、46種すべてを確認するまでに6箱の調査を要した。
これがツいてたのかツいてなかったのかを、シミュレーションで検討。
実際の商品と同数個のピースを含む架空のたべっ子どうぶつをプログラムし。
全種がそろうまでの開封・集計過程を10000回繰り返した。

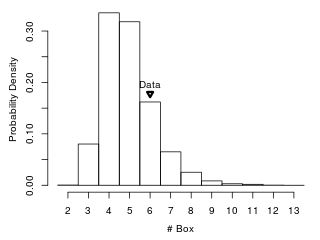
下記ヒストグラムは、シミュレーションにおいてかかった箱数の分布。
横軸が、調査開始から全種そろうまでにかかる箱の数。
縦軸がその箱数でそろう頻度。

ひと箱の枚数は45枚程度なので。
どんなに幸運でも、1箱で全46種そろえるのはほぼ不可能。
運がよければ2・3箱でそろう可能性もあるが。
平均的には、4ないし5箱でそろうことが多かった。

よって、実データにおける6箱というのは、やや不運な部類。
言い換えれば、実データでは出る種がやや偏っていたと考えられる。

ひと箱に含まれる種数

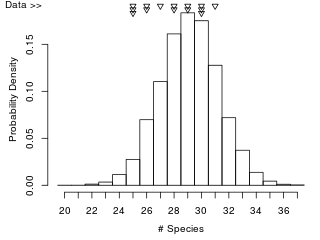
同様のシミュレーションで、ひと箱に含まれる種数を集計。
横軸がひと箱内に含まれるどうぶつの種数。
縦軸が頻度。
上部の三角形は、実際の各回集計における結果。

シミュレーション上は、ひと箱に29種含まれることがもっとも多く。
それを中心に、左右対称な釣鐘状分布をとった。
いっぽう実データは、29種よりも少ない種数しか含まれないことが多く。
やはり実際の商品では、どうぶつがやや偏る傾向が表われている。

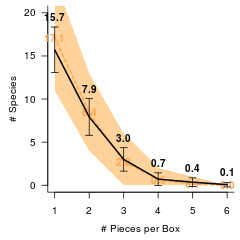
ひと箱に含まれる枚数とその種数

ひと箱で何種のどうぶつに何枚のダブりが生じるのかを検討。
横軸がひと箱内における同一ピースの数。
縦軸がその枚数ダブる種の数。
橙色の背景はシミュレーションによる平均と95%信頼区間。
黒の実線は実データにおける平均と標準偏差。

たとえば理論的には、ひと箱に1枚しか入っていない種は17種強。
3枚入っているどうぶつは2.7種いると読み取れる。
ここで実データは、シミュレーションより傾きが若干緩やか。
つまり少数枚入っている種が少なく、そのぶん多数枚ダブる種が多い。

たとえば
という現象は、理論上はほとんどない（50箱に1回ある程度）。
しかし実際の調査では、6箱めで遭遇した。
ここでもやはり、実商品で内容が偏る傾向がみてとれる。

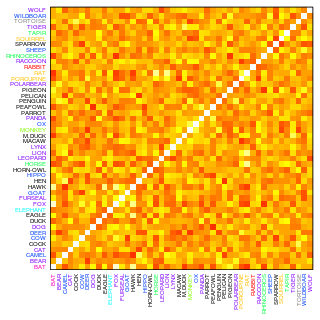
2種間のピース数相関

種間の同時出現関係を調べるため、箱あたりのピース数の相関を検討。
任意の2種について、Spearmanの方法によりひと箱内の個数の相関を計算。
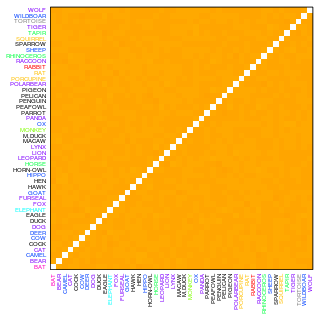
計算された全組み合わせの相関係数行列をカラーマップで表示した。

明るいセルほど相関係数が大きいことを示しており。
すなわち、ひと箱内に行の種が多いとき、列の種も多くみつかり易い。
相関係数は独立・従属変数の順に因らないので、マップは対角線に対称。
対角上は同種間なので100%相関。

このままでは共存しやすいグループ構造の有無がわかりにくい。
そこで、各箱に含まれていた各種のピース数の集計表から対応分析を実施。
種得点の第1軸の値をもとに、相関係数行列を並べ替えた。
（ホントは主成分分析などにかけたいが、サンプルが小さく困難。）

対応分析により、共変動関係にある種が近傍に並べ替えられるため。
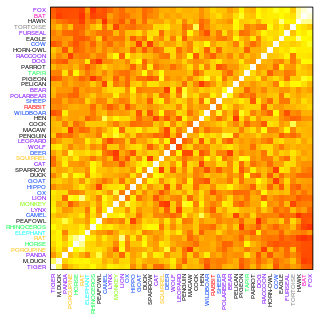
カラーマップの対角に、相関係数が相互に高い種がグループとして集まった。
たとえばBATとFOXとHAWK。
これらの種は、いずれかが箱に含まると、他の種も含まれやすいといえる。

しかしこうした種間のグループ化は、系統関係とは無関係のようにみえる。
すなわち「鳥類同士はピース数が相関する」といった明らかな傾向はない。
またたべっ子どうぶつには、ピース形状がほとんど同じ種が存在するが。
（e.g. OXとCOW，COCKとHEN）
それらのあいだにも、とくに高い相関関係があるとは限らない。

以上から、種間のピース数相関にも、一貫した法則性はないようである。
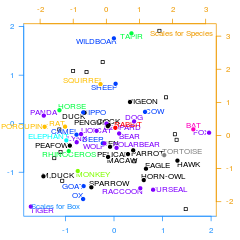
ちなみに対応分析の第1・2軸の結果をそのまま示すと下図のようになり。
やはりはっきりとしたクラスタ構造はいまのところみられない。

ただし種間相関が完全にゼロであれば、カラーマップは対角以外一様となるはず。
たとえばシミュレーションデータにおける相関係数行列は以下のとおり。
実データにみられた相関のパターンは、仮想データほど一様ではない。
これが小サンプルゆえの単なるノイズか否かは、さらなる検討が必要だ。

ひと箱のピース数のばらつきと種間のピース重量

サンプル間におけるピース数のばらつきも検討を要する。
本研究において、ひと箱のピース数は平均45個程度だったが。
箱ごとに1ないし2個前後の数の違いがみられた。
つまりたべっ子どうぶつは、封入個数の厳密な管理はされていない。

このことから、内容量は数ではなく重さで規格化されている可能性が高い。
製品外箱記載の情報では、たべっ子どうぶつの内容量は63グラム。
おそらく製造時には、重さを計測しながら包装袋にビスケットを投入し。
規定の重量が入ったところで封をしていると考えられる。

この場合、個々の製品個体の内容重量は統一されるが。
ピースの数がそろうとは限らない。
というのも、たべっ子どうぶつのピースは種ごとに形が違っており。
ものによっては、一見してわかるほど大きさが違う種もある。
よって必然的に、1ピースあたりの重さもまちまちだと予想される。

たまたま小さい（重量として軽い）種が多く入った個体では。
内容重量を統一するためには、より多くのピースが必要となり。
そのせいで箱ごとのピース数にばらつきが生じうる。

ここで、この内容重量の管理の精度を検証したい。
といっても、本研究では内容量の重さは計測していないため。
直接的にそれを検証することはできない。
また、そうした内容量の直接的な計測検証は、ともすれば
といったクレーム的な主張に聞こえかねないが。
それは本研究の本意ではない。

本解析では、小標本における限られた種の出現頻度情報をもとに。
製造過程における制約条件を考察することを目的とする。

前提として、ひと箱は平均45個で63グラムなので。
1ピースあたりの重さは約1.4グラムのはずだ。
ここで製造時に、45ピースで63グラムをわずかに下回った場合を考える。
重量規定を満たすためには、さらにピースを追加する必要があるが。
その追加ピースの重さは、現重量と規定重量の差に近いほど望ましく。
うっかり重い種を追加すると、逆に内容量がグラム単位で超過してしまう。

このように、ひと箱中の枚数のばらつきは、重量での封入制御を示唆するが。
重さを一定に保つには、種間の1ピース重量の違いを利用する必要があり。
追加するピースと現重量のあいだに、制約関係がうまれる。
言い換えれば、内容枚数が多い箱では1ピースが軽い種が多く。
逆に枚数が少ない箱では、1ピースが重い種が多くなっているはずである。

こうした関係の有無の検討には、各種の1ピースの重量を知る必要があるが。
一枚いちまいのピースは非常に軽く、その重量を正確に量るのは困難である。
そこで本研究では、まずひと箱の内容重量が一定という仮定をおき。
そのもとで逆に各種のピース重量を推定し、推定値の妥当性を検討した。

任意の種iにおいて、1ピースの重量をw[i]、箱に入っていた枚数をn[i]とする。
ひと箱のサンプルにおける総重量は、
と表わせる。
左辺は1ピースあたりの重さと枚数の積の総和であり。
右辺の63はひと箱のグラム数だ。

全種分46個の未知のw[i]を求めるには、46元の連立方程式を解けばよい。
しかし、直接これを行なうには、46箱のサンプリングを行なう必要があり。
またそれをしたとしても、一意な解が得られるとは限らない。

そこで本研究では、実際に調査した限られたサンプルのデータをもとに。
すべての箱の重量を一定にできる各種の重さの最適なセットを計算機的に推定した。
最適化計算にはRのoptim関数を用いた。
すべての種について、1ピース重量の初期値は1.4グラムとし。
計算された箱ごとの総重量が63グラムに近づくよう、各種の重量を調整した。

推定計算の妥当性を検討するため。
まず全データからひと箱ぶんをテストデータとして除外し。
残りのデータを用いて、46種の各ピースの重量を推定。
その推定された値を用いて、テストデータのひと箱の重さを算出し。
推定結果の未知データへの適用可能性を検討した。

これをテストに使う箱を替えて全サンプル分行なった。
結果は以下のグラフのとおりである。

横軸はテストデータとした箱のインデックス。
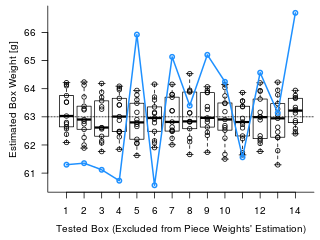
縦軸は箱ごとの重さで。
青色はテストデータの重量。
箱ひげ図は推定計算につかった他の箱の重量の推定値である。

たとえば、第1回調査のデータをテストデータとした場合。
第1回以外のデータから各ピースの重さを推定し。
結果、推定につかった箱の重量の中央値は63gに収束させられたが。
そのピース重量を使うと、残された第1回の箱の重量は61g程度となり。
規定重量から逸脱してしまうことがわかる。
（図左端 x = 1 のデータ）

全体をみても、やはり青線は箱ひげ図からかなり離れている。
つまり、ひと箱ごとの重量を規定値に近付けるという観点では、
であることを示している。

このように、ピース重量推定に使った箱は63gに近づけられるが。
その推定値では、新規の箱重量は規定値に近付けられないことがわかった。
このことはすなわち、本解析においてとった
という仮定が誤りであったことを示唆する。

このように本製品には、重量の規格化のために種を選別した証拠はなく。
封入時の重量制約は、どの種が封入されるかには影響しないとおもわれる。

その他

どうぶつリストにおけるASCIIコード順との食い違い

たべっ子どうぶつのパッケージ裏には、どうぶつのリストが載っており。
英語名順で、BATからWOLFまで46種の英・和名が羅列されている。

こどもの英語教育にはうってつけのこのリストだが。
一部のどうぶつについてだけ、なぜかアルファベット順と少し違っている。
当該部分は以下の3箇所。
（[表記順] → [ASCIIコードにおける正しい順]）

• [MACAW - M,DUCK] → [M,DUCK - MACAW]
• [PENGUIN - PELICAN] → [PELICAN - PENGUIN]
• [RAT - RABBIT - RACCOON] → [RABBIT - RACCOON - RAT]

カンマが含まれるM,DUCKが変則なのはまだわかるとしても。
他の二者については、なぜこの順になっているのか謎である。
これら以外は、すべて英語名のアルファベット順でソートされているため。
「なぜココだけ…」という疑問が一層深まる。

いずれにしても、これらの種についてはリストの順がASCII順ではないので。
Rのfactor関数などで水準化する際、気をつけないと順序が変わってしまう。
解析時には注意が必要である。

ちなみに、ソートがカタカナの読みでされている可能性も考えたが。
「コック」と振られたCOCKのうしろに「カウ」のCOWが置かれていたり。
「ドッグ DOG」のうしろに「ダック DUCK」だったりすることから。
上記3箇所の逸脱部以外はアルファベット順なのは間違いないだろう。

HORSEの入っていない可能性は低いか

ギンビス公式Twitterが、2014年（午年）の元日に
というようなツイートをしていた。
そのなかで
なる発言があったのだが、これは本当だろうか。

前述のとおり、たべっ子どうぶつには46種のピースがある。
ひと箱に含まれるピース数を、とりあえずn個とすると。
「46種から1種を無作為に箱に放り込む」をn回繰り返すことを考える。

1回の試行でHORSE以外を封入する確率は(45 / 46)なので。
それを独立にn回繰り返してしまう確率は、
によって計算できる。
集計によると、ひと箱に含まれるピース数は45枚程度だから、
の確率で、HORSEが入っていない。

べつの考え方をしてみる。
ひと箱に含まれる種の数をr種とする。
全46種からr種を選ぶ組み合わせは
である。
うちHORSEを含まないのは、HORSE以外の45種から選んだ
の組み合わせである。

後者を前者で割れば、大部分は約分できて
と考えられる。
シミュレーションによれば、ひと箱には平均29種が含まれるから
となり、前述の計算結果とほぼ一致する。

こうして得られた
という事実に照らし合わせて、公式Twitterの
なる発言が正確と考えるかは、ひとそれぞれだろう。

まあたしかに、確率としては50%を切っているので。
ある意味で「可能性は少ない」のかもしれない。
しかしたとえば、ツイートにより100人が商品を購入すれば。
うち37人は「ご容赦ください」な現象をくらうわけである。

そもそもが何に対して「比較的」なのかも不明なので。
かかる発言がどういう意図でなされたのか、よくわからないが。
個人的には37%を「少ない」と呼ぶのは違和感を覚える。

OXとCOWは両方入っているのか

Yahoo知恵袋で、
という質問をみかけた。

これはたぶん、
を聞いている質問。
なので答としては
で必要十分。

しかし、もしかして質問者は
を聞きたかったのではないだろうか。
…というまったく無用な気遣いをしてみる。

計算してみよう。
1パックにおけるOXとCOWの入りかたのパターンは、

• OXもCOWも入っている ... (1)
• OXは入っているがCOWは入っていない ... (2)
• OXは入っていないがCOWは入っている ... (3)
• OXもCOWも入っていない ... (4)

の4通り。

(1)の確率を知りたいわけだが。
(2)～(4)のほうが計算しやすいので。
それを計算してから余事象をとる。
簡単のため、1箱のピース数を45個とする。
どうぶつの種類は46種。

(4)の「OXもCOWも入っていない」パターンは、
だから、
となる。

つぎに(2)の「OXが入っててCOWはない」確率。
まずCOWが入っていない確率を考える。
COW以外の45種から45個封入される場合だから
となる。
じつは上記のHORSE問題でやった計算とおなじ。
（封入確率は等しい前提なので、ピース種で違いがない。）

ただ、これはOXもないケース（つまり(4)）を含んでいる。
なのでそういうパターンを除外して、
が「OXはあるけどCOWはない」となる確率。

先述のとおり、ピース種は計算に無関係なので。
(3)の「OXなしCOWあり」も、(2)とまったくおなじ。
23.7%。

これら以外が(1)の「OX・COW両方ある」場合なので。
確率1から(2)～(4)を引いて、
の確率で、1箱内にOXとCOWが揃う。
（小数第1位は丸め誤差。）

例によってシミュレーションも。
架空のたべっ子どうぶつ10000箱で調べてみる。
結果、OXとCOWのあり/なしの分割表は

• OXあり COWあり ... 4106箱
• OXあり COWなし ... 2277箱
• OXなし COWあり ... 2359箱
• OXなし COWなし ... 1258箱

となった。

ばらつきが大きいけど、おおむね理論値どおり。
シミュレーションを増やせば理論値に近づいた。

ついでに
の二値ではなく、
で確率をプロットしてみる。
さらに誰にも求められていない情報である。

底面の2軸が、OXとCOWの個数の組み合わせ。
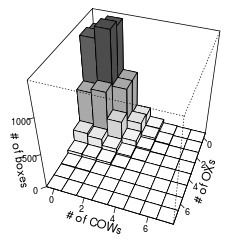
それが起こった回数が棒の高さ。
「OX・COWが1個ずつ」がもっとも起こりやすいが。
「2個ずつ」となると、一気に数%まで確率が下がり。
「3個ずつ」とかなると奇跡的。